
L’idea dell’automa
cellulare (AC) è vecchia approssimativamente quanto il calcolatore elettronico
digitale.
Le prime ricerche
furono condotte da John Von Neumann (con un importante contributo di Stanislaw
Ulam) nei primi anni cinquanta.
L’obiettivo
principale di Von Neumann era escogitare un semplice sistema capace di
riprodursi alla maniera di un organismo vivente.
Anche il più noto
automa cellulare, il gioco vita
inventato nel 1970 da John Horton Conway, ha un aspetto biologico, come
suggerisce il nome; le cellule nascono, vivono o muoiono a seconda della densità
della popolazione locale.
Un automa cellulare può
essere visto come una matrice virtualmente illimitata di celle in uno spazio
n - dimensionale (nella maggior parte delle applicazioni lo spazio è a
due dimensioni e le celle sono quadrate). Le celle evolvono in un tempo
immaginario, scandito da un orologio interno all’automa cellulare. A ogni
istante (t) ciascuna cella si trova in uno stato che appartiene ad un insieme
finito di stati possibili. Lo stato della cella al tempo (t+1) dipende oltre che
dal suo stato al tempo (t), anche dallo stato delle celle del proprio intorno al
tempo (t), in funzione di un determinato set di regole.
Ad ogni passaggio è
così possibile osservare le trasformazioni che si verificano a livello di
sistema e indagare sulle interazioni locali che hanno determinato queste
trasformazioni.
Tecnicamente gli
elementi che costituiscono un automa cellulare sono quattro:
1.
L’insieme di stati di una cella
L’insieme A di stati
che può assumere una cella contiene almeno due elementi. Tali stati sono le
caratteristiche assunte dalle porzioni di spazio dello scenario dell’automa
(le celle).
Ogni stato Si è
caratterizzato da un numero d’ordine N, da un valore o caratteristica
semantica V, eventualmente da un colore C, eventualmente da un valore numerico
H.
Possono essere
definiti degli stati speciali, come il bordo dello scenario o lo stato
qualsiasi, per un loro uso particolare nelle regole di trasformazione. Se in una
regola compare lo stato bordo, il riconoscimento della cella bordo ha la
precedenza sullo stato effettivo della regola. Se in una regola compare lo stato
qualsiasi, non viene valutato lo stato effettivo di tale cella.

2.
L’intorno di analisi della cella
L’intorno di analisi
è l’insieme delle celle dello scenario, in riferimento ad una data cella,
che viene considerato nelle regole di trasformazione. Nella letteratura
sugli automi cellulari sono definiti diversi intorni: nel caso bidimensionale i
più famosi sono quelli di Moore, di
Von Neumann e di Margolus. (Figura 2.1)
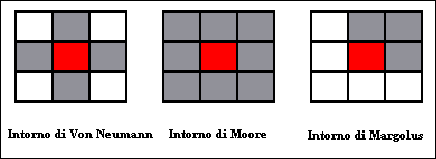
Figura 2.1 – Esempi di intorni
La cella rossa è la
cella attiva, le celle grigie sono le celle dell'intorno che devono essere prese
in considerazione nelle regole di variazione, le celle bianche sono le celle
dell'intorno che non devono essere prese in considerazione nelle regole di
variazione.
Si possono considerare
anche intorni a più livelli.
In un automa
cellulare, per valutare la variazione delle celle, può essere significativo
limitare l'intorno di analisi solo ad un sottoinsieme di celle.
3.
Le regole di trasformazione della cella
Le regole di
trasformazione di una cella prescrivono il cambiamento dello stato di una cella
in base a diversi parametri: lo stato corrente della cella, lo stato delle celle
di un intorno associato alla regola, eventuali condizioni di esclusione di
valori per gli stati delle celle dell’intorno, alcune condizioni speciali,
frequenza di applicazione della regola, probabilità di applicazione della
regola.
Se k è il numero di
stati per cella ed n è il numero di celle incluse nell’intorno, vi sono ((k)k)n
possibili regole [7].
Per un automa binario,
quindi, nell’intorno di Von Neumann (dove n è 4) ci sono più di 65000
possibili regole; nell’intorno di Moore (dove n è 8) ve ne sono 1077.
Nelle applicazioni reali il numero di regole è sensibilmente inferiore a quello
potenziale, poiché solo una piccola parte di esse è utile per spiegare le
trasformazioni di un particolare fenomeno.
La forma generale di
una regola è quindi la seguente:
Ri
= r [ S(t), S(t+1),
I, N, Ek, F, P]
dove:
S(t) = stato della cella alla t - esima transizione;
I = stati
delle celle dell’intorno;
N = stati di eventuale
esclusione dall’intorno;
Ek =
condizioni speciali;
F = frequenza di
applicazione;
P = probabilità
di applicazione;
Le condizioni speciali
possono dipendere dalla presenza complessiva delle celle di un determinato
stato:
La regola speciale E1
è ad esempio eseguita se il numero di celle dello stato Si al tempo
di
Se non sono previste
condizioni speciali, la regola può essere eseguita sempre (nel rispetto del
soddisfacimento degli altri parametri di applicazione).
La frequenza F di
esecuzione di una regola può essere indicata con un numero compreso tra 0 e
100. Questo parametro permette di stabilire la percentuale di celle attive sul
numero totale di celle potenzialmente attivabili, che possiedono cioè tutti i
requisiti per trasformarsi da una scansione all’altra.
La probabilità P di
esecuzione di una regola può essere un numero compreso tra 0 e 1. Questo
parametro agisce in cascata rispetto a quello di frequenza e permette di
stabilire la percentuale di celle che si trasformano, sul numero totale di celle
attivate dalla frequenza.
4.
Lo scenario
Lo scenario di un
automa cellulare è generalmente una griglia bidimensionale omogenea di celle
rettangolari, quadrate o esagonali. La dimensione dello scenario è quindi
determinata dal prodotto delle celle presenti nella larghezza per le celle
presenti nella lunghezza. Uno scenario può essere visto come una matrice di
valori definiti come:
Ki
= k (i, j, v)
essendo i, j le
coordinate di una cella nel sistema adottato per lo scenario e v(i, j) lo stato
assunto dalla cella.
Un campo di
particolare interesse, oltre allo studio dei comportamenti degli ecosistemi, in
cui sono stati costruiti modelli euristici basati sugli automi cellulari è
stato quello dell’analisi territoriale. Si tratta di un problema complesso,
difficilmente riconducibile ad una teoria, in quanto le variabili tipiche di un
sistema territoriale, come la popolazione o gli insediamenti produttivi, non si
distribuiscono in modo continuo ed uniforme, ma si concentrano in agglomerati di
differenti dimensioni e strutture.
Le prime applicazioni
ai sistemi urbani riguardano modelli probabilistici di simulazione dei processi
di crescita urbana sviluppati da Chapin negli anni sessanta (Chapin e Weiss,
1968). La modellizzazione dello sviluppo urbano di Detroit attraverso lo spazio
cellulare è stata dimostrata da Tobler (1970) e le stesse idee sono state
successivamente sostenute da Couclelis (1985) in una simulazione del ciclo di
sviluppo di una città ideale. Couclelis proponeva l’utilizzo di modelli di
automi cellulari urbani come metafore
della crescita urbana piuttosto che come veri simulatori.
Negli anni ‘90, con
il crescente interesse verso le dinamiche spazio - temporali e la teoria dei
frattali, sono state ottenute applicazioni più realistiche, con il contributo
di diversi ricercatori, tra i quali: White e Engelen (1993), Cecchini e Viola
(1992), Batty e Xie (1997).
Il comune denominatore
di tutte le più recenti applicazioni è l’utilizzo di griglie bidimensionali,
un numero ridotto di celle, solitamente inferiore a 6400, e un limitato numero
di scansioni, fino a 50. Nei sistemi urbani è poco probabile che intorni di
primo livello possano indurre effetti spaziali necessari per una buona
simulazione; in tutti i casi, si è quindi utilizzato un intorno molto più
esteso, spesso di oltre 5 celle di distanza dalla cella attiva.
Sia Tobler (1979), che
Couclelis (1985), che Batty (1997), definiscono alcuni principi che gli automi
cellulari ortodossi dovrebbero
seguire, ma che, a loro avviso, occorre necessariamente rilassare per costruire
modelli applicabili al settore urbanistico.
Le convenzioni di
fondo che accomunano i modelli di automi cellulari classici sono [11]:
1.
definizione di un piano (spazio) infinito;
2.
stazionarietà spaziale degli intorni;
3.
regolarità nelle forme;
4.
omogeneità spaziale;
5.
invarianza spaziale e temporale delle regole;
6.
chiusura rispetto ad eventi esterni;
7.
regolarità temporale.
Per regolarità nelle
forme si intende che la griglia è formata da celle uguali in dimensione e
disegno; per omogeneità spaziale si intende che le forme e gli stati possibili
per una cella sono gli stessi in tutto lo spazio; per chiusura si intende che
l’evoluzione del sistema non può essere influenzata da altro che dai suoi
meccanismi; per regolarità temporale si intende che il tempo deve scorrere
uniformemente.
Affinché i modelli
urbani e regionali basati sugli automi cellulari possano essere utili per le
previsioni si debbono verificare due condizioni:
1.
l’interattività, essenziale per l’esplorazione di opzioni;
2.
il realismo, sia rispetto ai dati che rispetto alla struttura del
modello.
Conseguenza della
ricerca di realismo nella struttura del modello è la necessità di rilassare i
principi ortodossi proposti.
La figura 2.2 mette a confronto le ipotesi di fondo degli automi cellulari classici con quelle rilassate in prospettiva di un utilizzo più realistico degli automi cellulari urbani.
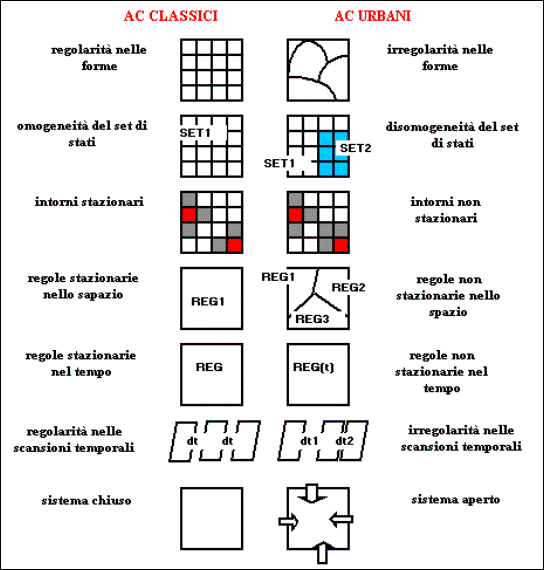
Figura 2.2 – Confronto tra automi cellulari classici e automi
cellulari urbani secondo Couclelis
(1985)
AUGH2! (Automi Urbani
Generalizzati con Help! in linea) è un sistema per la costruzione di automi
cellulari di diversi tipi attraverso una interfaccia utente semplice ed
efficiente.
AUGH2! è stato
realizzato dal Laboratorio di Ricerca e Laurea STRATEMA dell’Istituto
Universitario di Architettura di Venezia, Dipartimento di Analisi Economica e
Sociale del Territorio, nell’ambito di una ricerca pluriennale riguardante gli
automi cellulari come metodologia di simulazione di fenomeni dinamici
ambientali.
Il sistema AUGH2! è
stato sviluppato con il linguaggio di programmazione Prolog. La versione di
Prolog adottata è la WIN-PROLOG prodotta dalla Logic Programming Associated
(LPA) di Londra.
AUGH2! possiede le
seguenti caratteristiche:
1)
la topologia dello
spazio cellulare (scenario) dell'automa è di due tipi: piana e toroidale;
2)
le dimensioni dello
spazio cellulare sono due;
3)
il comportamento ai
confini dell'automa è di due tipi: a scomparsa ed a bordi interagenti;
4)
la geometria dello
spazio è un rettangolo (dimensioni: base x altezza);
5)
la tessitura dello
spazio è quadrata (lo spazio è suddiviso in celle di forma quadrata);
6)
il numero di stati
della cella possibili varia da un minimo di due ad un massimo di n (n è dipendente dall'implementazione);
7)
l'intorno di
analisi è variabile (può comprendere tutte le celle a tutti i livelli
dell’intorno, come un sottoinsieme di esse) e può essere profondo fino a cinque
livelli;
8)
la morfologia
dell'automa è monocellulare;
9)
la scansione dello
spazio cellulare produce un effetto immediato sequenziale;
10)
l’estensione delle
regole è globale (le regole di trasformazione della cella vengono applicate a
tutto lo spazio cellulare nel medesimo modo).
Il motore per la
esecuzione degli automi cellulari del sistema AUGH2! è un algoritmo che
consiste fondamentalmente nella procedura di analisi dello spazio cellulare
(scenario) e della sua trasformazione.
Tale algoritmo si può
riassumere sinteticamente nei seguenti passi.
1. Inizializzazione dell'automa
Questa fase comprende
l’installazione delle componenti dell'automa che si vuole eseguire, necessarie
alla sua esecuzione: caricamento dello scenario, dell'intorno di analisi, dell’
insieme di stati della cella e delle regole di trasformazione.
2. Analisi e trasformazione dello spazio
cellulare
Quando l'automa è stato installato, può essere eseguito con un determinato numero di cicli di scansione dello spazio cellulare. Ogni ciclo di scansione è composto di due fasi: la fase di analisi e trasformazione dello spazio cellulare e la fase di disegno (visualizzazione) della trasformazione.
2.1. Analisi dello spazio cellulare
Nella fase di analisi
dello spazio cellulare di ciascun ciclo di scansione tutte le celle dello
scenario vengono analizzate, nell'ordine da sinistra verso destra e dall'alto
verso il basso. Per ognuna di queste celle, il motore effettua le azioni di
analisi della cella e del suo intorno, valutazione della sua variazione e
memorizzazione della variazione.
2.1.1. Analisi della cella e del suo intorno
Viene analizzato lo
stato della cella e lo stato delle celle nell'intorno della cella stessa.
2.1.2. Valutazione della variazione della cella
Viene cercata una regola
di trasformazione la cui prima parte (stato della cella e dell'intorno) abbia
corrispondenza con lo stato della cella dello scenario che si sta analizzando e
del suo intorno. Se viene trovata una regola di questo tipo, la cella
considerata subisce una variazione di stato come prescritto dalla regola, se
vengono soddisfatte anche le condizioni di esclusione, le condizioni speciali e
di frequenza di attivazione e probabilità.
2.1.3. Memorizzazione della variazione
L'eventuale nuovo stato della cella viene memorizzato in un database temporaneo, in attesa che venga analizzato tutto lo spazio cellulare.
2.2. Disegno (visualizzazione) della
trasformazione dello spazio cellulare
2.2.1. Aggiornamento del database delle celle
dello scenario
Quando tutte le celle
dello scenario sono state analizzate si procede alla loro trasformazione,
sostituendo con il nuovo stato (precedentemente memorizzato nel database
temporaneo) il vecchio stato nelle celle che hanno subito la variazione.
2.2.2. Visualizzazione della trasformazione dello
spazio
Tutto lo scenario viene
ridisegnato, con i nuovi stati delle celle, ancora nell'ordine da sinistra
verso destra e dall'alto verso il basso. Con l'operazione di ridisegno e la
cancellazione del database temporaneo dei nuovi stati delle celle termina il
ciclo di scansione dello spazio cellulare, e può iniziarne un altro, se ne
rimangono da eseguire, oppure l’esecuzione dell'automa può terminare.
La costruzione di un
automa cellulare è definita in AUGH2! come la costruzione di un progetto. Ogni
progetto è costituito dai quattro elementi caratterizzanti l’automa cellulare:
un insieme di stati, un insieme di regole, un intorno di analisi ed uno
scenario.
Questi elementi non
possono essere assemblati liberamente, ma devono sottostare a gerarchie che
derivano dalla dipendenza esistente tra gli elementi stessi.
La dipendenza riguarda
le seguenti coppie di elementi:
Insieme
di stati della cella : Regole di variazione.
Insieme
di stati della cella : Scenari.
Intorni di analisi : Regole di variazione.
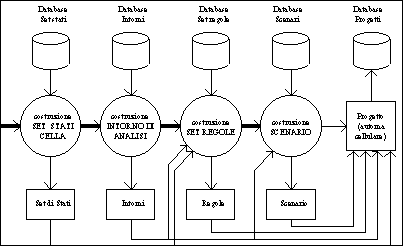
Figura 2.3. -
Fasi di costruzione di un progetto con AUGH2!
Non possono essere
definite regole se non è stato scelto un insieme di stati; non può essere
costruito uno scenario senza la scelta di un insieme di stati, e non possono
essere definite regole senza la scelta di un intorno di analisi.
In ragione di queste
dipendenze, la costruzione di un Progetto è una costruzione guidata, nel senso
che viene richiesto all'utente di definire inizialmente l’insieme di stati
della cella, poi di definire l'intorno di analisi, e successivamente di
costruire le regole di variazione e lo scenario.
Oltre alla possibilità
di costruire un automa cellulare tramite la definizione di un progetto, il
sistema AUGH2! permette la gestione di più progetti in cascata, attraverso il
multiautoma.
Si definisce multiautoma un automa cellulare
complesso, costituito da due o più automi cellulari concatenati in sequenza, in
modo tale che l’output prodotto da un automa (usualmente uno scenario) diventi
l’input dell’automa successivo nella sequenza. Un multiautoma è quindi definito
fondamentalmente da un nome e da una lista degli automi cellulari componenti la
sequenza:
<NOME MULTIAUTOMA>
<Nome Automa 1>
.....
<Nome Automa i>
.....
<Nome Automa n>
Gli elementi componenti
i singoli automi diventano gli elementi del multiautoma. Così, stati della
cella, intorni, regole e scenario degli automi diventano elementi del
multiautoma, con una sola restrizione: deve essere definito un unico insieme di
stati della cella per tutti gli automi, che diventa lo stato della cella del
multiautoma. Il motivo di ciò è dato dal fatto che un unico scenario viene
elaborato, dai diversi automi, dall’inizio alla fine della sequenza, quindi non
possono essere presenti insieme di stati diversi da quello relativo allo
scenario di trasformazione.
Per convenzione, si
considera come insieme di stati di riferimento quello del primo automa in
sequenza, e come scenario di partenza anche quello del primo automa.
Più in dettaglio, gli
elementi dei singoli automi della sequenza multiautoma sono i seguenti:
Automa 1 …. Automa
i ….. Automa n
Insieme stati 1 …. Insieme stati i …. Insieme stati n
Intorni 1 …. Intorni
i …. Intorni n
Insieme regole 1 …. Insieme
regole i …. Insieme regole n
Scenario 1 …. Scenario
i …. Scenario n
Intorni e insieme di regole degli automi componenti dovranno quindi essere compatibili con l’insieme di stati scelto per il multiautoma. Lo scenario elaborato da un automa della sequenza diventa lo scenario da elaborare dal prossimo automa nella sequenza. Nella descrizione considerata si ha:
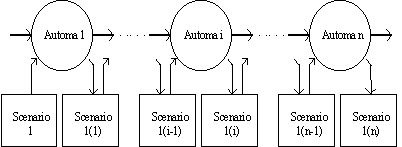
Figura 2.4. - Schema di un multiautoma
L’esecuzione di un
multiautoma corrisponde all’esecuzione in cascata degli automi componenti la
sequenza. Ogni automa può essere eseguito per uno o più cicli, a discrezione
dell’utente.
Un limite di AUGH2! è infatti quello di non essere in grado di autogestire il numero di scansioni ma di richiederlo all’utente. E’ quindi quest’ultimo a stabilire quando terminare l’esecuzione del progetto e, nel caso del multiautoma, quando far avvenire la transizione da un progetto al successivo.