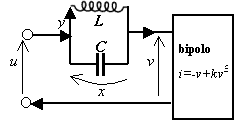
Simuliamo il semplice circuito elettrico illustrato in figura, attraverso il programma PPLANE che è disponibile su: http://www.elet.polimi.it/Users/DEI/Sections/Automation/Giorgio.Guariso/appunti/software/pplane.html. 

Assumendo, come si fa di solito, la tensione sul condensatore come variabile di stato x, la corrente come variabile di stato y e data la caratteristica del bipolo non lineare, le equazioni del sistema sono:

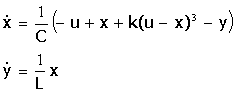
Si tratta dunque di un sistema del secondo ordine, per la simulazione del quale PPLANE offre molte possibilità interessanti.

Cominciamo col definire le equazioni nella prima schermata, assumendo per semplicità uº 0 e L=C=k=1 (figura 1) Parametri diversi non comporterebbero nessuna differenza o difficoltà.

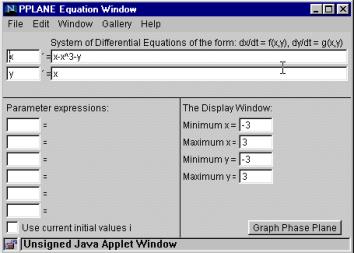
Figura 1 - Finestra di definizione delle equazioni. Si decide di visualizzare lo spazio di stato tra   -3 e 3 per entrambe le variabili.
 
 
 
 
 
 

Appena terminata questa operazione, ci appare il quadro di stato con il vettore traiettoria, calcolato in ogni punto di una griglia (questa opzione di default può essere esclusa mediante il pulsante "Direction field settings", tra le opzioni).

Fissando con il mouse un punto qualsiasi dello spazio di stato, otteniamo la traiettoria che passa da esso (figura 2a). Per visualizzare il corrispondente movimento (figura 2b), si sceglie un'opzione  (ad esempio "Both x-t & y-t" del menu Graph). Inoltre, volendo calcolare un punto di equilibrio, si sceglie l'opzione "Find an equilibrium point" dal menu Solution, insieme ad uno stato attorno al quale effettuare la ricerca (sempre usando il mouse sul quadro di stato).

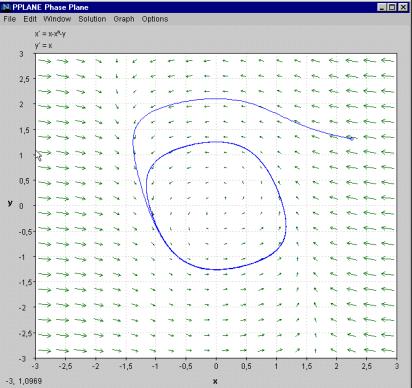
Figura 2a - Finestra del quadro di stato, con tracciata una traiettoria.

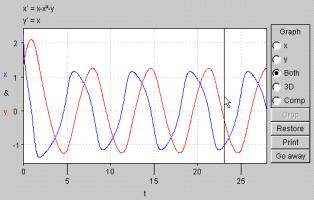
Figura 2b - Il movimento corrispondente alla traiettoria in figura 2a.
 
 
 
 
 
 
 
 
 
 

Le coordinate dei punti di equilibrio appaiono, insieme allo Jacobiano valutato in esso ed ai relativi autovalori in una piccola finestra numerica (figura 3).

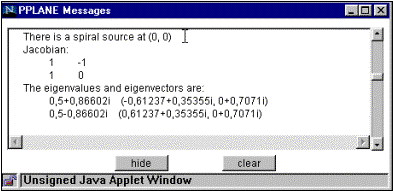
Figura 3 - Finestra delle caratteristiche (tipo, posizione, Jacobiano, autovalori) dello stato di equilibrio.
 
 
 
 

Utilizzando la procedura di ricerca dell'equilibrio per il caso in esame e tracciando qualche traiettoria (attenzione che per default sono tracciate anche le traiettorie all'indietro, cioè per t negativo; questa caratteristica può essere tolta dall'opzione "Soluction direction" nel menu Options) si può ottenere la situazione riportata in figura 4.

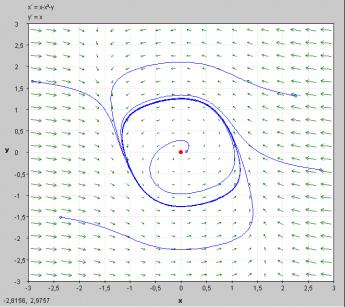
Figura 4 - Equilibrio e traiettorie del sistema in esame.
 
 
 
 
 
 
 
 

Come si vede, c'è una regione circolare del piano che attira le traiettorie, le quali, partendo sia all'esterno che all'interno di questa regione, tendono a convergere su di essa. Analizzando il movimento di entrambe le variabili di stato (vedi ancora 2b), si nota che esso tende a diventare periodico, qualsiasi sia lo stato iniziale. Si deduce quindi che, al confine delle due regioni, l'una dove il movimento tende ad allontanarsi dall'origine (che è un fuoco instabile) e l'altra in cui il movimento tende invece a tornare verso l'andamento periodico, ci deve essere una traiettoria limite corrispondente a un ciclo. Partendo da un punto qualsiasi di questa traiettoria, si deve poter ritornare in esso, dopo un opportuno periodo di tempo. Approssimativamente questo periodo può essere stimato, dopo che è trascorso un transitorio sufficientemente lungo dall'istante iniziale, prendendo l'intervallo tra due valori uguali nel grafico del movimento (nel nostro caso quindi, circa 6,5 unità di tempo).

La stima che si ottiene in questo modo, così come la rappresentazione che si ha sul quadro di stato, sono tuttavia soltanto approssimazioni del ciclo reale. Quest'ultimo è una traiettoria particolare nel piano e quindi, per essere simulata, richiederebbe una precisione infinita. Ciò che invece accade è che, anche se si riuscisse a partire, per un colpo di fortuna (che tuttavia ha probabilità nulla di verificarsi) da un punto del ciclo, al primo passo di simulazione ci si ritroverebbe al di fuori di esso, qualsiasi sia l'algoritmo (PPLANE ne mette a disposizione due nel menu Options -ODE solver) o il passo (che si può scegliere nella finestra che appare dopo la scelta dell'algoritmo) adottati.

Tuttavia, quello che accade nel caso in esame è che l'errore introdotto dalla simulazione viene, in qualche modo, "corretto" dalla struttura stessa del sistema, che tende a riportare tutte le traiettorie sul ciclo (che appunto per questo viene detto stabile).

A queste conclusioni si poteva arrivare anche con considerazioni basate sulla fisica del sistema: per valori piccoli di y (il termine -v³ è trascurabile rispetto a v) il bipolo, si comporta come una resistenza negativa, cioè fornisce energia al sistema.

Al contrario, per valori elevati di v, dove il termine -v³ diventa prevalente, il bipolo sottrae energia al sistema, ancora più di un normale resistore. Deve esistere quindi una condizione limite in cui queste due tendenze si bilanciano ed essa è appunto costituita dal ciclo che abbiamo trovato.

Le approssimazioni (e le debolezze) della simulazione sono messe ancora meglio in evidenza se immaginiamo di invertire il comportamento del bipolo cambiandone i segni. Esso si comporterà, in questo caso, come una normale resistenza per valori piccoli di i e fornirà invece energia per valori elevati.

Il quadro delle traiettorie che otteniamo in questo caso (figura 5a) rimane vuoto in una corona circolare attorno all'equilibrio, perché tutte le traiettorie che cerchiamo di far partire da quella zona tendono ad allontanarsi da essa. Ciò ci rende impossibile, via simulazione, "vedere" la traiettoria limite, cioè il ciclo, che in questo caso è instabile (si vedano i movimenti in figura 5b). Notate che modificare l'algoritmo o il passo non può cambiare la situazione perché, ancora una volta, anche se si partisse da un punto del ciclo, al successivo passo di simulazione si sarebbe comunque fuori di esso.

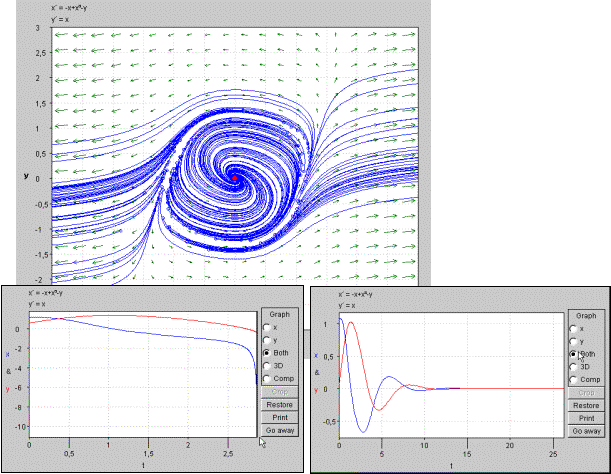
Figura 5a - Equilibrio e traiettorie del sistema col bipolo cambiato di segno: l'equilibrio è ora un fuoco stabile e il ciclo è instabile.
 
 
 
 
 
 
 
 
 
 

Figura 5b - Movimenti corrispondenti a due stati iniziali molto vicini, uno all'esterno e uno all'interno del ciclo.