 Richiami di teoria sul modello gaussiano
Richiami di teoria sul modello gaussiano
tratto da Finzi, Brusasca "La qualità dell'aria", Masson,
Milano, 1991
Indice
1.
Calcolo della concentrazione con il modello gaussiano
1.1
Modello gaussiano standard
1.2
Modello gaussiano con terreno riflettente
1.3
Modello gaussiano in presenza di inversioni in quota
2. Stabilità
atmosferica
Tabella
delle classi di stabilità
3.
Profilo verticale della velocità del vento
Tabella
degli esponenti della funzione che rappresenta il profilo della velocità
del vento
4.
Altezza effettiva della sorgente
4.1
Pennacchi galleggianti
4.2 Pennacchi
tipo jet
5.
Determinazione dei coefficienti di dispersione
5.1
"Pasquill-Gifford"
5.2
"Brookhaven National Laboratory"
5.3
"Tennessee Valley Authority"
5.4 "Briggs
open-country" e "Briggs urban"
6. Elenco
dei simboli utilizzati
1.
Calcolo della concentrazione con il modello gaussiano
1.1
Modello gaussiano standard
Il calcolo della concentrazione
è stato effettuato basandosi sul modello gaussiano derivato, con
opportune ipotesi semplificative, dalla soluzione dell’equazione di diffusione:
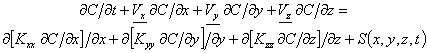 (1)
(1)
dove:
C (x,y,z,t)=
concentrazione di inquinante nel punto di coordinate (x,y,z),
al tempo t
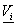 =
velocità media del vento nella direzione i (i = x,
y, z)
=
velocità media del vento nella direzione i (i = x,
y, z)
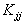 =
coefficiente di diffusione turbolenta nella direzione jj
(jj
= xx, yy, zz)
=
coefficiente di diffusione turbolenta nella direzione jj
(jj
= xx, yy, zz)
S(x,y,z,t)=
portata della sorgente di inquinante nel punto di coordinate (x,y,z),
al tempo t
Le ipotesi semplificative assunte
per il caso in esame sono le seguenti:
-
il processo è stazionario
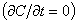
-
il vento è costante nel tempo
e nello spazio, e con intensità non nulla solo lungo la direzione
x
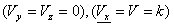
-
nella direzione x, il trasporto dovuto
al vento è preminente rispetto a quello dovuto alla turbolenza
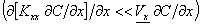
-
i coefficienti di diffusione,
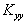 e
e 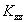 ,
sono costanti in y
e z
,
sono costanti in y
e z
-
la sorgente è costante nel tempo
e puntiforme, con valore non nullo (pari a Q) solamente nel punto
di coordinate (0,0,0).
L’equazione (1) diviene di conseguenza:
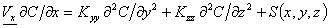
 (2)
Con le opportune condizioni al contorno:
(2)
Con le opportune condizioni al contorno:
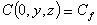 per
per 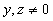
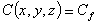 per
per 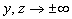 ,
la soluzione analitica risulta
essere:
,
la soluzione analitica risulta
essere:
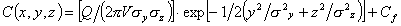 (3)
ovvero una gaussiana doppia, con deviazioni
standard
(3)
ovvero una gaussiana doppia, con deviazioni
standard 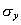 e
e 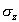 ,
essendo
,
essendo 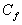 la
concentrazione di fondo di inquinante in atmosfera,
la
concentrazione di fondo di inquinante in atmosfera,
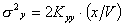 ,
, 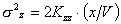 (4)
L’equazione (3) presuppone quindi
che la sorgente di inquinante sia posta nell’origine degli assi coordinati,
e che la diffusione possa avvenire indefinitamente verso l’alto e verso
il basso.
(4)
L’equazione (3) presuppone quindi
che la sorgente di inquinante sia posta nell’origine degli assi coordinati,
e che la diffusione possa avvenire indefinitamente verso l’alto e verso
il basso.
Nella realtà bisogna tenere
conto della presenza del terreno, che riflette parte dell’inquinante, per
cui si procede a modificare opportunamente l’equazione (3).
Ritorna all'indice
1.2
Modello gaussiano con terreno riflettente
Si suppone che l’emissione
avvenga ad una quota z=He (essendo He
l’altezza effettiva della sorgente), e si considera il suolo totalmente
riflettente nei confronti delle particelle di inquinante che lo raggiungono.
Il contributo dato dalla riflessione
si può immaginare equivalente a quello dato da una sorgente virtuale
posta alla quota z=-He , per cui l’equazione
(3) assume la seguente forma:
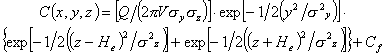 (5)
(5)
Una formulazione analoga si otterrà
anche nel caso in cui si consideri la presenza di strati di inversione
termica e di inversione in quota, come verrà mostrato successivamente.
Per mostrare la diversa distribuzione
di inquinante che risulta dalle eq. (3) e (5), si propongono di seguito
due esempi di risultati ottenibili.
In questo caso si ignora
la presenza del terreno, per cui la distribuzione di inquinante risulta
simmetrica, lungo la direzione x, rispetto alla sorgente.
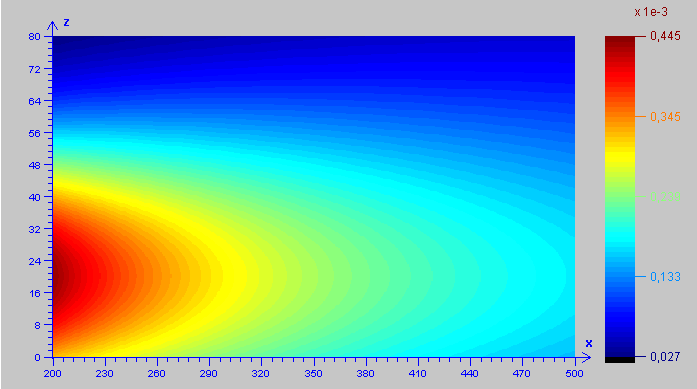
Figura 1 – Distribuzione
derivante dal modello gaussiano standard
In
quest’altro caso, invece (senza variare i parametri), si prende in considerazione
la presenza del terreno, e lo si considera totalmente riflettente. Risulta
evidente il contributo della sorgente virtuale posta alla quota z=-He
.
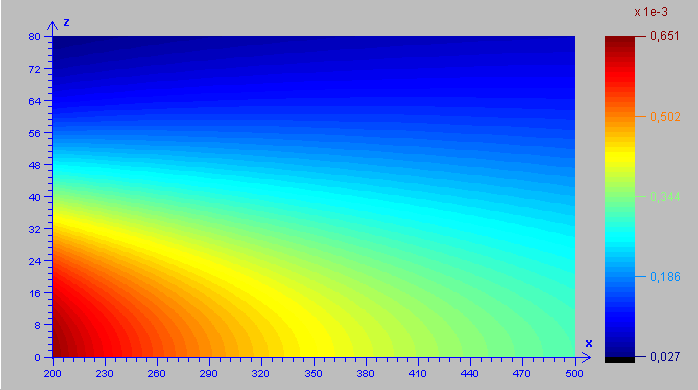
Figura 2 - Distribuzione
derivante dal modello gaussiano con terreno riflettente
Per la determinazione dei parametri
presenti nell’equazione (ovvero 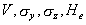 )
si
è fatto riferimento ad alcune delle metodologie più accettate
in letteratura, riportate nelle sezioni successive.
)
si
è fatto riferimento ad alcune delle metodologie più accettate
in letteratura, riportate nelle sezioni successive.
Ritorna all'indice
1.3
Modello gaussiano in presenza di inversioni in quota
La trattazione è
simile alla precedente, considerando però che il pennacchio non
è più libero di espandersi indefinitamente verso l’alto.
Si può estendere il modello
utilizzato per tener conto della riflessione al suolo, valutando ora la
presenza di un secondo strato riflettente, in quota; il pennacchio continuerà
a rimbalzare tra i due strati, e la formulazione corretta per definire
la concentrazione risulta quindi la seguente:
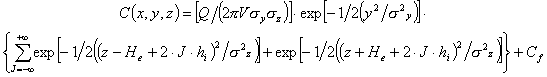 (6)
essendo
(6)
essendo 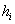 la
quota dello strato di inversione.
la
quota dello strato di inversione.
Come si può notare, la formula
assume la presenza di infinite sorgenti virtuali, poste a quota 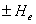 (J=0),
(J=0), 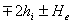 (
(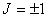 ),
e così via.
),
e così via.
La serie converge generalmente
con pochi termini (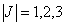 ),
e la distribuzione verticale della concentrazione di inquinante tende ad
uniformarsi allontanandosi dalla sorgente. E’ quindi ragionevole considerarla
uniforme al di là di un certo valore della coordinata x.
),
e la distribuzione verticale della concentrazione di inquinante tende ad
uniformarsi allontanandosi dalla sorgente. E’ quindi ragionevole considerarla
uniforme al di là di un certo valore della coordinata x.
Se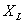 è la distanza a cui il pennacchio raggiunge per la prima volta lo
strato di inversione, si assume costante la distribuzione verticale per
è la distanza a cui il pennacchio raggiunge per la prima volta lo
strato di inversione, si assume costante la distribuzione verticale per 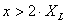 ,
ottenendo la formulazione seguente:
,
ottenendo la formulazione seguente:
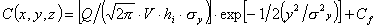 (7)
(7)
Per definire il valore di 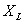 ,
si assume convenzionalmente che il bordo del pennacchio sia definito da
una concentrazione pari a 1/10 di quella massima (centrale), e si ricava
che
,
si assume convenzionalmente che il bordo del pennacchio sia definito da
una concentrazione pari a 1/10 di quella massima (centrale), e si ricava
che 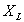 è
quella distanza per cui
è
quella distanza per cui
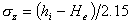 (8).
(8).
Quindi, si utilizza la formula (6)
fino alla distanza 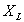 ,
la (7) oltre la distanza
,
la (7) oltre la distanza 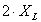 ,
e un’interpolazione tra le due per le distanze intermedie.
,
e un’interpolazione tra le due per le distanze intermedie.
Un esempio dei risultati
ottenuti è mostrato nella seguente immagine, in cui è possibile
apprezzare la fase di transizione tra le zone a distribuzione verticale
uniforme e variabile (corrispondente approssimativamente all’intervallo
205 £x
£410m).
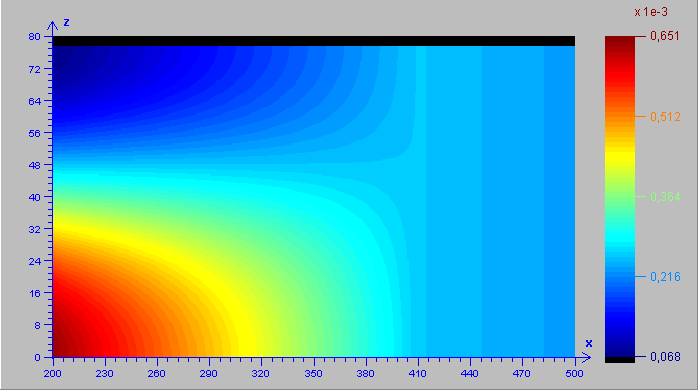
Figura 3 - Distribuzione derivante
dal modello gaussiano, con terreno riflettente e strato di inversione in
quota
Ritorna all'indice
2. Stabilità
atmosferica
Il gradiente di temperatura adiabatico
è definito da
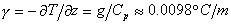 (9)
essendo
(9)
essendo
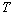 =
temperatura
della particella d’aria
=
temperatura
della particella d’aria
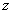 =
quota
della particella
=
quota
della particella
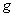 =
accelerazione
di gravità
=
accelerazione
di gravità
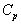 =
calore specifico a pressione costante
=
calore specifico a pressione costante
In caso di atmosfera neutra si ha quindi
una diminuzione di circa 1°C ogni 100 m di quota.
Si possono definire le seguenti
situazioni di stabilità:
Il gradiente termico dell’atmosfera
è minore di quello adiabatico, situazione tipica nel periodo diurno.
Il moto verticale delle particelle d’aria viene quindi amplificato, per
cui si ha una elevata dispersione verticale.
Il gradiente termico è
prossimo a quello adiabatico, per cui si ha una situazione di equilibrio
per le particelle.
Il gradiente termico dell’atmosfera
è maggiore di quello adiabatico, per cui vengono smorzati eventuali
movimenti verticali delle particelle d’aria. Si ha quindi una dispersione
verticale ridotta.
-
inversione termica in quota
Si ricade in questo caso se si
è in presenza di uno strato d’aria in cui la temperatura aumenta
con la quota. In tale condizione può essere impedita la diffusione
verso l’alto delle particelle, che restano intrappolate al di sotto di
tale strato limite, con conseguente aumento della concentrazione al suolo.
Se lo strato di inversione è
a una quota inferiore a quella di emissione, la situazione è duale
rispetto alla precedente, e le particelle di inquinante vengono riflesse
verso l’alto, senza raggiungere il suolo.
Per schematizzare le varie categorie
di stabilità, si fa generalmente ricorso alla seguente corrispondenza:
Tabella
1 – Categorie di stabilità atmosferica
|
Categoria di stabilità
|
Situazione atmosferica
|
|
A
|
condizioni estremamente instabili
|
|
B
|
condizioni moderatamente instabili
|
|
C
|
condizioni leggermente instabili
|
|
D
|
condizioni neutre
|
|
E
|
condizioni leggermente stabili
|
|
F
|
condizioni stabili
|
Ritorna all'indice
3.
Profilo verticale della velocità del vento (V)
Il profilo verticale della velocità
del vento è un parametro influenzato dalla rugosità del terreno
e dalla situazione di stabilità atmosferica.
Si considerano in genere due possibilità:
velocità del vento costante con la quota, oppure variabile.
Nel primo caso si assume la velocità
del vento costante a qualsiasi quota, pari a quella rilevata nel punto
di emissione dell’inquinante.
Nel secondo caso, basandosi sulla
velocità alla quota di emissione, si applica un’equazione di tipo
esponenziale per calcolarla ad una quota generica:
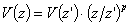 (10)
(10)
dove:
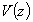 =
velocità del vento alla generica quota z
=
velocità del vento alla generica quota z
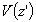 =
velocità del vento misurata alla quota z',
assunta pari alla quota di emissione.
=
velocità del vento misurata alla quota z',
assunta pari alla quota di emissione.
L’esponente p è definito
in funzione della stabilità atmosferica e della rugosità
del terreno, ed i valori utilizzati sono riportati nella seguente tabella:
Tabella
2 – Valori di p, in funzione della rugosità del terreno e ella stabilità
atmosferica

Alla quota del terreno la velocità
risulta nulla; per evitare che le equazioni (3, 5, 6, 7) utilizzate per
il calcolo della concentrazione divergano, si assume:
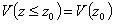 .
.
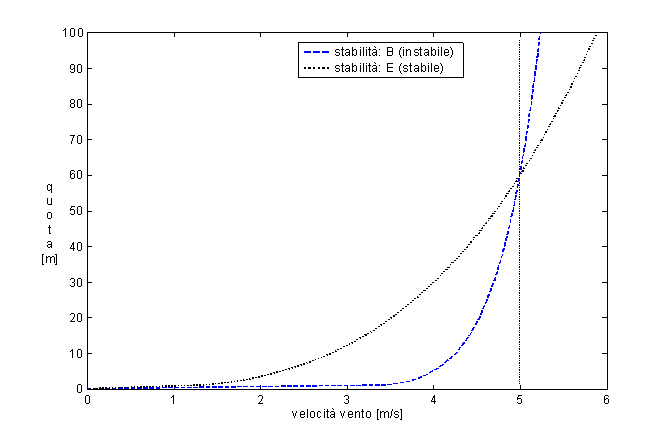
Le variazioni del profilo verticale
della velocità del vento diminuiscono spostandosi verso situazioni
atmosferiche di maggiore instabilità, come si può verificare
nel grafico seguente, ottenuto considerando due casi esemplificativi (velocità
vento = 5 m/s alla quota di 60m; rugosità terreno = 0.10 m; classi
di stabilità atmosferica: B, E).
Figura 4 – Variazione del profilo
verticale della velocità del vento, in funzione della stabilità
atmosferica
Ritorna all'indice
4.
Altezza effettiva della sorgente (He)
All’uscita dalla ciminiera il pennacchio
di fumo è soggetto ad una fase di innalzamento, transizionale, e
ad una in cui si può considerare livellato, ovvero con l’altezza
del baricentro costante.
Il parametro He ,
altezza
effettiva della sorgente, è definito come l’altezza a cui il pennacchio
raggiunge la situazione di livellamento (convenzionalmente, quando la pendenza
scende al di sotto del 5%).
He è
data dalla somma di due componenti: l’altezza geometrica della sorgente
e il sovrainnalzamento:
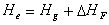 (11)
Si considerano generalmente due categorie
principali di pennacchi:
(11)
Si considerano generalmente due categorie
principali di pennacchi:
-
galleggianti (l’innalzamento è
dovuto principalmente al galleggiamento del gas)
-
jet (prevale il termine cinetico, dovuto
all’elevata velocità di efflusso del gas)
Si trascurano, in questa trattazione,
i possibili effetti scia della ciminiera e/o degli edifici circostanti,
significativi, rispettivamente, in caso di rapporto tra velocità
di uscita e velocità del vento minore di 1.5, e di rapporto tra
altezza della ciminiera e degli edifici minore di 2.5 .
Ritorna all'indice
4.1 Pennacchi
galleggianti
Rientrano in questa categoria i pennacchi
caratterizzati da masse elevate, con temperatura dei fumi maggiore di quella
ambiente. La massa elevata ostacola il rimescolamento con l’atmosfera,
e determina un innalzamento che si protrae per un periodo piuttosto prolungato.
Si è utilizzata la formula
di Briggs, che definisce l’innalzamento pari a:
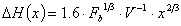 (12)
(12)
essendo
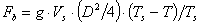 (13)
(13)
definito come "parametro di galleggiamento"
(Ts è la temperatura dei fumi, T la temperatura
dell’aria, D il diametro terminale della ciminiera).
4.1.1 Atmosfera neutra
Per quanto riguarda la distanza a cui
l’asse del pennacchio si può considerare livellato, si distinguono
due sottocasi:
-
Hg
minore o uguale a 305m:
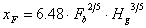 (14)
(14)
-
Hg maggiore
di 305m:
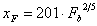 (15)
(15)
Il sovrainnalzamento massimo risulta
essere:
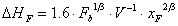 (16)
Nella simulazione, si è utilizzata
tale formulazione anche per il caso di atmosfera instabile.
(16)
Nella simulazione, si è utilizzata
tale formulazione anche per il caso di atmosfera instabile.
4.1.2 Atmosfera stabile
In questo caso si effettua una distinzione
basata sulla velocità del vento:
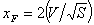 (17)
(17)
quindi
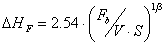 (18),
(18),
essendo
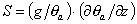 definito
come "parametro di stabilità dell’atmosfera";
definito
come "parametro di stabilità dell’atmosfera";
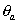 è
la temperatura potenziale dell’aria, ovvero la temperatura che la particella
d’aria assume se viene portata adiabaticamente ad una pressione di riferimento
di 1000 hPa;
è
la temperatura potenziale dell’aria, ovvero la temperatura che la particella
d’aria assume se viene portata adiabaticamente ad una pressione di riferimento
di 1000 hPa;
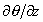 assume
valore nullo nel caso di atmosfera neutra, valori positivi per atmosfera
stabile e negativi per atmosfera instabile.
assume
valore nullo nel caso di atmosfera neutra, valori positivi per atmosfera
stabile e negativi per atmosfera instabile.
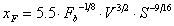 (19)
quindi
(19)
quindi
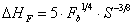 (20),
(20),
4.1.3 Atmosfera instabile
Si utilizza la formula seguente:
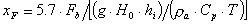 (21),
dove
(21),
dove
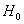 =
flusso di calore sensibile al suolo
=
flusso di calore sensibile al suolo
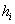 =
altezza dello strato di rimescolamento
=
altezza dello strato di rimescolamento
Ritorna all'indice
4.2 Pennacchi
tipo jet
Fanno parte di queste categoria i pennacchi
per cui il sovrainnalzamento è dovuto principalmente ad una elevata
velocità di efflusso dei fumi.
La formula di Briggs è in
questo caso la seguente:
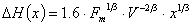 (22)
(22)
essendo
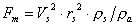 (23)
(23)
definito come "parametro di flusso
inerziale" (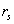 è
il raggio della ciminiera,
è
il raggio della ciminiera, 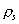 e
e 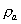 sono
le densità dei fumi e dell’aria).
sono
le densità dei fumi e dell’aria).
Avendo maggior importanza la velocità
del fumo rispetto alla sua temperatura, si può considerare 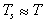 ,
e quindi
,
e quindi 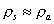 ,
per cui è possibile semplificare l’espressione utilizzata.
,
per cui è possibile semplificare l’espressione utilizzata.
Nella definizione dell’innalzamento
massimo si distinguono due sottocasi:
-
in presenza di vento:
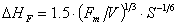 (24)
(24)
-
in assenza di vento:
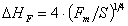 (25)
(25)
4.2.1 Presenza di uno strato di inversione in
quota
Se è presente uno strato di
inversione in quota, è possibile che il sovrainnalzamento del pennacchio
venga ostacolato.
L’inversione è caratterizzata
da una quota iniziale e da una finale (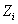 ,
, 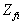 ),
e da una escursione termica (
),
e da una escursione termica (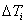 ).
).
Si indica con 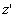 l’altezza
massima raggiungibile dal pennacchio nelle condizioni di inversione presenti,
e la si ricava dalle seguenti equazioni:
l’altezza
massima raggiungibile dal pennacchio nelle condizioni di inversione presenti,
e la si ricava dalle seguenti equazioni:
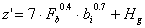 ,
per
,
per 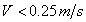 (26)
(26)
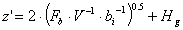 ,
per
,
per 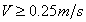 (27)
essendo
(27)
essendo
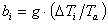 (28)
Il pennacchio è in grado di
superare lo strato di inversione se
(28)
Il pennacchio è in grado di
superare lo strato di inversione se 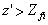 ,
oppure se
,
oppure se 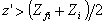 nel caso di strato di inversione con notevole estensione verticale; se
tali condizioni non sono verificate, resterà confinato al di sotto
dello strato limite.
nel caso di strato di inversione con notevole estensione verticale; se
tali condizioni non sono verificate, resterà confinato al di sotto
dello strato limite.
Ritorna all'indice
5.
Determinazione dei coefficienti di dispersione (sye
sz)
I coefficienti di dispersione, sye
sz,
sono i parametri che determinano la dispersione dei fumi nell’atmosfera.
I valori da essi assunti sono condizionati
dalla situazione di stabilità atmosferica e dalla coordinata x in
corrispondenza della quale vengono valutati. Tali valori tendono ad aumentare
con la distanza e con l’instabilità.
Vi sono vari modelli generalmente
utilizzati per il calcolo; nel nostro caso si sono considerati i seguenti:
-
"Pasquill-Gifford"
-
"Brookhaven National Laboratory"
-
"Tennessee Valley Authority"
-
"Briggs open-country" e "Briggs
urban".
5.1 Pasquill-Gifford
E’ generalmente utilizzato in condizioni
di terreno relativamente piatto (aperta campagna), con sorgenti a bassa
quota (< 80m), ed ha la seguente formulazione:
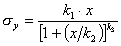 ,
,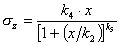 ,
(29)
,
(29)
con i valori delle costanti 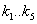 definiti
nella seguente tabella:
definiti
nella seguente tabella:
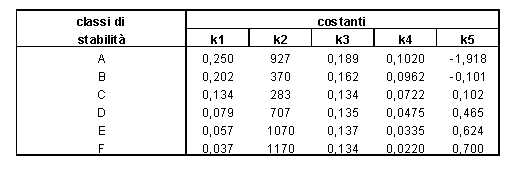
Tabella 3 – Valori delle costanti
per il calcolo della dispersione con il modello "Pasquill-Gifford"
5.2 Brookhaven National
Laboratory (BNL)
Utilizza un minor numero di categorie
di stabilità rispetto al modello di Pasquill, con la seguente corrispondenza
(Pasquill-Gifford) Þ
(BNL):
A Þ
(B2) , (B) Þ
(B1) , (C,D,E) Þ
(C) , (F) Þ
(D).
La formulazione è del
tipo:
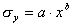 ,
, 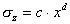 ,
(30)
,
(30)
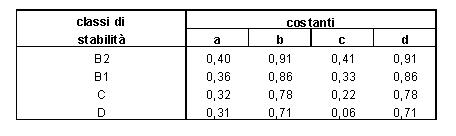
con i valori delle costanti a,b,c,d
definiti nella tabella 4.
Tabella 4 - Valori delle costanti
per il calcolo della dispersione con il modello "BNL"
5.3 Tennessee
Valley Authority (TVA)
E’ indicato per grandi impianti
di potenza a carbone situati in aperta campagna; si considera come velocità
del vento la media tra quella alla quota di emissione e quella alla quota
massima raggiunta dal pennacchio.
Si distinguono solamente due condizioni
di stabilità, e la formulazione è la seguente:
-
condizioni neutrali:
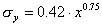 ,
, 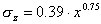 (31)
(31)
-
condizioni stabili:
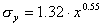 ,
, 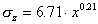 (32)
(32)
5.4 Briggs open-country,
Briggs urban
Le formule sono ottenute dalla
combinazione dei tre modelli precedenti, operando una distinzione tra diffusione
su terreni con coefficiente di rugosità ridotto (Briggs open-country)
o elevato (Briggs urban).
Le formulazioni sono riportate nelle
Tabelle 5 e 6.
Tabella 5 - Formule per il calcolo
della dispersione con il modello "Briggs open-country"
|
Briggs open-country
|
|
Categoria di stabilità
|
sy
|
sz
|
|
A
|
0.22x (1 + 0.0001x)-1/2
|
0.20x
|
|
B
|
0.16x (1 + 0.0001x)-1/2
|
0.12x
|
|
C
|
0.11x (1 + 0.0001x)-1/2
|
0.08x (1 + 0.0002x)-1/2
|
|
D
|
0.08x (1 + 0.0001x)-1/2
|
0.06x (1 + 0.0015)-1/2
|
|
E
|
0.06x (1 + 0.0001x)-1/2
|
0.03x (1 + 0.0003x)-1
|
|
F
|
0.04x (1 + 0.0001x)-1/2
|
0.016x (1 + 0.0003x)-1
|
Tabella 6 - Formule per il calcolo
della dispersione con il modello "Briggs urban"
|
Briggs urban
|
|
Categoria di stabilità
|
sy
|
sz
|
|
A – B
|
0.32x (1 + 0.0004x)-1/2
|
0.24x (1 + 0.0001x)-1/2
|
|
C
|
0.22x (1 + 0.0004x)-1/2
|
0.20x
|
|
D
|
0.16x (1 + 0.0004x)-1/2
|
0.14x (1 + 0.0003x)-1
|
|
E - F
|
0.11x (1 + 0.0004x)-1/2
|
0.08x (1 + 0.00015x)-1
|
Ritorna all'indice
6.
Elenco dei simboli utilizzati
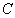 :
concentrazione di inquinante
:
concentrazione di inquinante
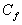 :
concentrazione di fondo di inquinante in atmosfera
:
concentrazione di fondo di inquinante in atmosfera
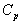 :
calore specifico a pressione costante
:
calore specifico a pressione costante
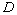 :
diametro terminale della ciminiera
:
diametro terminale della ciminiera
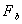 :
parametro di galleggiamento
:
parametro di galleggiamento
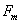 :
parametro di flusso inerziale
:
parametro di flusso inerziale
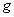 :
accelerazione di gravità
:
accelerazione di gravità
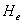 :
altezza effettiva della sorgente, pari a
:
altezza effettiva della sorgente, pari a 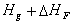
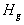 :
altezza geometrica della sorgente
:
altezza geometrica della sorgente
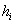 :
quota dello strato di inversione
:
quota dello strato di inversione
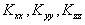 :
coefficiente di diffusione turbolenta nella direzione x,
y, z
:
coefficiente di diffusione turbolenta nella direzione x,
y, z
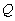 :
portata della sorgente
:
portata della sorgente
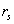 :
raggio terminale della ciminiera
:
raggio terminale della ciminiera
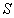 :
sorgente di inquinante
:
sorgente di inquinante
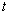 :
tempo
:
tempo
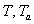 :
temperatura dell’aria
:
temperatura dell’aria
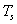 :
temperatura dei fumi
:
temperatura dei fumi
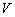 :
velocità media del vento
:
velocità media del vento
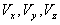 :
velocità media del vento nella direzione x,
y, z
:
velocità media del vento nella direzione x,
y, z
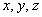 :
coordinate spaziali (x:
orizzontale, direzione vento; y:
orizzontale, ortogonale a x;
z:
verticale)
:
coordinate spaziali (x:
orizzontale, direzione vento; y:
orizzontale, ortogonale a x;
z:
verticale)
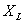 :
valori della coordinata x
per cui il pennacchio di fumo raggiunge lo strato di inversione in quota
:
valori della coordinata x
per cui il pennacchio di fumo raggiunge lo strato di inversione in quota
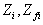 :
altezza iniziale e finale di uno strato di inversione
:
altezza iniziale e finale di uno strato di inversione
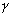 :
gradiente di temperatura adiabatico dell’aria
:
gradiente di temperatura adiabatico dell’aria
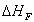 :
sovrainnalzamento massimo del pennacchio
:
sovrainnalzamento massimo del pennacchio
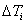 :
escursione termica di uno strato di inversione
:
escursione termica di uno strato di inversione
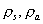 :
densità dei fumi e dell’aria
:
densità dei fumi e dell’aria
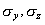 :
coefficienti di dispersione
:
coefficienti di dispersione
Ritorna all'indice
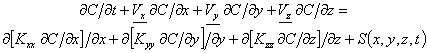 (1)
(1)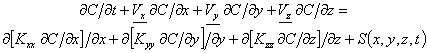 (1)
(1)= velocità media del vento nella direzione i (i = x, y, z)
= coefficiente di diffusione turbolenta nella direzione jj (jj = xx, yy, zz)
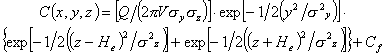 (5)
(5)

![]() )
si
è fatto riferimento ad alcune delle metodologie più accettate
in letteratura, riportate nelle sezioni successive.
)
si
è fatto riferimento ad alcune delle metodologie più accettate
in letteratura, riportate nelle sezioni successive.
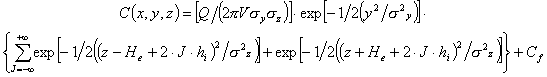 (6)
(6)![]() (J=0),
(J=0), ![]() (
(![]() ),
e così via.
),
e così via.
![]() ),
e la distribuzione verticale della concentrazione di inquinante tende ad
uniformarsi allontanandosi dalla sorgente. E’ quindi ragionevole considerarla
uniforme al di là di un certo valore della coordinata x.
),
e la distribuzione verticale della concentrazione di inquinante tende ad
uniformarsi allontanandosi dalla sorgente. E’ quindi ragionevole considerarla
uniforme al di là di un certo valore della coordinata x.
![]() è la distanza a cui il pennacchio raggiunge per la prima volta lo
strato di inversione, si assume costante la distribuzione verticale per
è la distanza a cui il pennacchio raggiunge per la prima volta lo
strato di inversione, si assume costante la distribuzione verticale per ![]() ,
ottenendo la formulazione seguente:
,
ottenendo la formulazione seguente:
(7)
(8).

= temperatura della particella d’aria
= quota della particella
= accelerazione di gravità
= calore specifico a pressione costante


![]() è
la temperatura potenziale dell’aria, ovvero la temperatura che la particella
d’aria assume se viene portata adiabaticamente ad una pressione di riferimento
di 1000 hPa;
è
la temperatura potenziale dell’aria, ovvero la temperatura che la particella
d’aria assume se viene portata adiabaticamente ad una pressione di riferimento
di 1000 hPa;
![]() assume
valore nullo nel caso di atmosfera neutra, valori positivi per atmosfera
stabile e negativi per atmosfera instabile.
assume
valore nullo nel caso di atmosfera neutra, valori positivi per atmosfera
stabile e negativi per atmosfera instabile.(22)
(23)
![]() ,
,![]() ,
(29)
,
(29)
![]() definiti
nella seguente tabella:
definiti
nella seguente tabella:


![]() :
concentrazione di fondo di inquinante in atmosfera
:
concentrazione di fondo di inquinante in atmosfera
![]() :
calore specifico a pressione costante
:
calore specifico a pressione costante
![]() :
diametro terminale della ciminiera
:
diametro terminale della ciminiera
![]() :
parametro di galleggiamento
:
parametro di galleggiamento
![]() :
parametro di flusso inerziale
:
parametro di flusso inerziale
![]() :
accelerazione di gravità
:
accelerazione di gravità
![]() :
altezza effettiva della sorgente, pari a
:
altezza effettiva della sorgente, pari a ![]()
![]() :
altezza geometrica della sorgente
:
altezza geometrica della sorgente
![]() :
quota dello strato di inversione
:
quota dello strato di inversione
![]() :
coefficiente di diffusione turbolenta nella direzione x,
y, z
:
coefficiente di diffusione turbolenta nella direzione x,
y, z
![]() :
portata della sorgente
:
portata della sorgente
![]() :
raggio terminale della ciminiera
:
raggio terminale della ciminiera
![]() :
sorgente di inquinante
:
sorgente di inquinante
![]() :
tempo
:
tempo
![]() :
temperatura dell’aria
:
temperatura dell’aria
![]() :
temperatura dei fumi
:
temperatura dei fumi
![]() :
velocità media del vento
:
velocità media del vento
![]() :
velocità media del vento nella direzione x,
y, z
:
velocità media del vento nella direzione x,
y, z
![]() :
coordinate spaziali (x:
orizzontale, direzione vento; y:
orizzontale, ortogonale a x;
z:
verticale)
:
coordinate spaziali (x:
orizzontale, direzione vento; y:
orizzontale, ortogonale a x;
z:
verticale)
![]() :
valori della coordinata x
per cui il pennacchio di fumo raggiunge lo strato di inversione in quota
:
valori della coordinata x
per cui il pennacchio di fumo raggiunge lo strato di inversione in quota
![]() :
altezza iniziale e finale di uno strato di inversione
:
altezza iniziale e finale di uno strato di inversione
![]() :
gradiente di temperatura adiabatico dell’aria
:
gradiente di temperatura adiabatico dell’aria![]()
![]() :
sovrainnalzamento massimo del pennacchio
:
sovrainnalzamento massimo del pennacchio
![]() :
escursione termica di uno strato di inversione
:
escursione termica di uno strato di inversione
![]() :
densità dei fumi e dell’aria
:
densità dei fumi e dell’aria
![]() :
coefficienti di dispersione
:
coefficienti di dispersione