 Modello ARMA: (dall'inglese Auto Regressive-Moving
Average)
Modello ARMA: (dall'inglese Auto Regressive-Moving
Average)
|
 Automa di Moore: Sistema
dinamico lineare a tempo e stati discreti
Automa di Moore: Sistema
dinamico lineare a tempo e stati discreti
| x(t+1) = f(x(t),u(t)) |
| y(t) = h(x(t)) |
|
|
 Asintotica
stabilità, semplice stabilità e instabilità:Un
sistema lineare è asintoticamente stabile se e solo se
il suo movimento libero tende a zero per Asintotica
stabilità, semplice stabilità e instabilità:Un
sistema lineare è asintoticamente stabile se e solo se
il suo movimento libero tende a zero per  qualunque sia lo stato iniziale. Se, invece, il movimento libero è
limitato ma non tende a zero per qualche stato iniziale, il sistema
si dice semplicemente stabile. Infine, se il movimento libero
è illimitato per qualche stato iniziale il sistema è instabile.
qualunque sia lo stato iniziale. Se, invece, il movimento libero è
limitato ma non tende a zero per qualche stato iniziale, il sistema
si dice semplicemente stabile. Infine, se il movimento libero
è illimitato per qualche stato iniziale il sistema è instabile.
In generale, queste proprietà sono attribuibili ad uno stato
di equilibrio di un sistema (non lineare) e dipendono dal comportamento
dei movimenti perturbati che hanno origine in uno stato dell'intorno
dell'equilibrio.
|
 Campionamento
a frequenza differenziata: Modalità
di campionamento differente per le diverse variabili di un sistema. Campionamento
a frequenza differenziata: Modalità
di campionamento differente per le diverse variabili di un sistema. |
 Campionamento
asincrono: Modalità di campionamento
costante nel tempo e uguale per tutte le variabili, nella quale risultano
tra loro sfasati gli istanti di campionamento. Campionamento
asincrono: Modalità di campionamento
costante nel tempo e uguale per tutte le variabili, nella quale risultano
tra loro sfasati gli istanti di campionamento. |
 Campionamento
casuale e campionamento adattativo: Modalità
di campionamento in cui T (l'intervallo di campionamento) non è
costante nel tempo ed ha valori casuali o dipendenti dalla variabilità
del segnale (adattativo). Campionamento
casuale e campionamento adattativo: Modalità
di campionamento in cui T (l'intervallo di campionamento) non è
costante nel tempo ed ha valori casuali o dipendenti dalla variabilità
del segnale (adattativo). |
|
 Costante
di tempo:Inverso
dell'opposto di un autovalore (sistemi lineari continui) o del logaritmo
del modulo dell'autovalore (sistemi lineari discreti). Costante
di tempo:Inverso
dell'opposto di un autovalore (sistemi lineari continui) o del logaritmo
del modulo dell'autovalore (sistemi lineari discreti).
La funzione di trasferimento di un
sistema lineare continuo del primo ordine è
del tipo:
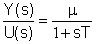
|
 Criterio
di instabilità della traccia: In un sistema a
tempo continuo [discreto] di dimensione n la traccia della matrice A
è positiva [maggiore di n in modulo] il sistema è
instabile. La dimostrazione di questa proprietà è ovvia,
se si ricorda che la traccia di una matrice è pari alla somma dei
suoi autovalori. Criterio
di instabilità della traccia: In un sistema a
tempo continuo [discreto] di dimensione n la traccia della matrice A
è positiva [maggiore di n in modulo] il sistema è
instabile. La dimostrazione di questa proprietà è ovvia,
se si ricorda che la traccia di una matrice è pari alla somma dei
suoi autovalori. |
 Criterio
di Poincarè: Esiste un ciclo stabile
in una corona delimitata da due linee chiuse C1 e C2 se tali linee sono
attraversate dalle traiettorie dall'esterno verso l'interno e se nella
corona non esistono stati di equilibrio. Criterio
di Poincarè: Esiste un ciclo stabile
in una corona delimitata da due linee chiuse C1 e C2 se tali linee sono
attraversate dalle traiettorie dall'esterno verso l'interno e se nella
corona non esistono stati di equilibrio. |
 Diagramma di Bode:
Diagramma cartesiano delle funzioni R(w)
e f(w), normalmente tracciato in scala logaritmica. Diagramma di Bode:
Diagramma cartesiano delle funzioni R(w)
e f(w), normalmente tracciato in scala logaritmica. |
 Diagramma
di Nyquist: Diagramma polare rappresentante la funzione Diagramma
di Nyquist: Diagramma polare rappresentante la funzione 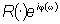 . . |
 Forma
canonica di controllo: Sistema di ordine
(n) pari alla "dimensione" della parte autoregressiva del modello ARMA. Forma
canonica di controllo: Sistema di ordine
(n) pari alla "dimensione" della parte autoregressiva del modello ARMA.
E' la quaterna
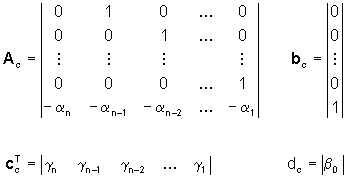
con
gi=bi-b0ai
i=1,…,n
che è una particolare realizzazione
di un assegnato modello ARMA (anche non ridotto)
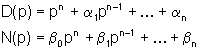
|
 Formula
di Lagrange: Formula
di Lagrange:
-
In un sistema lineare a tempo continuo
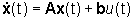 lo stato x(t) per
lo stato x(t) per 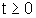 è dato da (formula di Lagrange):
è dato da (formula di Lagrange):
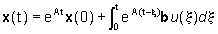
dove
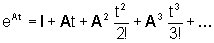
-
Analogamente, in un sistema lineare a tempo
discreto x(t+1)=Ax(t)+bu(t) per
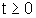 ,
vale la formula: ,
vale la formula:
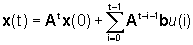
detta anch'essa formula di Lagrange.
|
 Formula
di Mason: Formula
di Mason:
La formula di Mason permette di calcolare
la funzione di trasferimento G(p) di un qualsiasi aggregato di sottosistemi.
Nell'ipotesi che nello schema che definisce l'aggregato siano usati solo
nodi sommatori (cioè nell'ipotesi che nell'aggregato vengano soltanto
effettuate somme tra segnali) la formula è la seguente
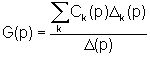
dove Ck(p), D(p)
e Dk(p)
si chiamano, rispettivamente, funzione di trasferimento del k-esimo
cammino diretto (cioè non contenente cicli) tra ingresso e uscita,
determinante
dell'aggregato, e determinante ridotto rispetto al k-esimo
cammino diretto. La funzione di trasferimento Ck(p)è
semplicemente il prodotto delle funzioni di trasferimento di tutti i sistemi
che costituiscono il k-esimo cammino diretto. Il determinante D(p)
è, invece, dato da
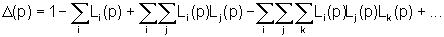
dove Li(p) è la funzione
di trasferimento dell'i-esimo cammino chiuso (anello), cioè
il prodotto delle funzioni di trasferimento di tutti i sistemi che costituiscono
l'i-esimo percorso chiuso esistente nell'aggregato. Nella formula,
la prima sommatoria è estesa a tutti gli anelli, la seconda alle
coppie di anelli disgiunti (cioè che non si toccano) e così
via. Infine, il determinante ridotto Dk
è
il determinante privato di tutti i termini relativi ad anelli non
disgiunti (cioè toccati) dal k-esimo cammino diretto. |
 Funzione
di trasferimento: Funzione
di trasferimento:
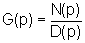 dove D(.)
e N(.) sono due polinomi di grado n
dove D(.)
e N(.) sono due polinomi di grado n
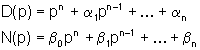
e p è un operatore di "anticipo"
nel caso di tempo discreto, (cioé py(t)=y(t+1), p2y(t)=y(t+2),
...) e di "derivazione" nel caso di tempo continuo (cioé 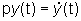 , , 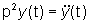 ,
...). ,
...). |
 Funzione
a
variazione limitata:una
funzione a valori reali Funzione
a
variazione limitata:una
funzione a valori reali 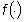 si dice a variazione limitata nell’intervallo chiuso [a,b] se esiste
una costante K tale che per ogni insieme finito di punti t0,t1,t2,.
. .,tn che partizionino l’intervallo [a,b] (a
= t0 < t1 < t2
<.
. .< tn=b) si abbia
si dice a variazione limitata nell’intervallo chiuso [a,b] se esiste
una costante K tale che per ogni insieme finito di punti t0,t1,t2,.
. .,tn che partizionino l’intervallo [a,b] (a
= t0 < t1 < t2
<.
. .< tn=b) si abbia
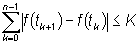 Se una funzione
Se una funzione 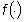 definita su R è a variazione limitata in ogni intervallo chiuso
si dice che tale funzione è a variazione limitata. Inoltre, una
funzione
definita su R è a variazione limitata in ogni intervallo chiuso
si dice che tale funzione è a variazione limitata. Inoltre, una
funzione 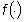 a valori complessi è detta a variazione limitata se la sua parte
reale e la sua parte immaginaria sono a variazione limitata.
a valori complessi è detta a variazione limitata se la sua parte
reale e la sua parte immaginaria sono a variazione limitata. |
 Guadagno:
Rapporto m
tra uscita e ingresso di un sistema
all'equilibrio Guadagno:
Rapporto m
tra uscita e ingresso di un sistema
all'equilibrio
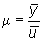
-
per i sistemi a tempo continuo vale la formula
m=d-cTA-1b
-
mentre per i sistemi a tempo discreto vale la formula
m=d+cT(I-A)-1b
|
 Intervallo
di campionamento: Intervallo di tempo
intercorrente tra due istanti successivi di campionamento . Intervallo
di campionamento: Intervallo di tempo
intercorrente tra due istanti successivi di campionamento . |
 Linearizzazione:
Approssimazione locale del funzionamento di un sistema dinamico,
mediante l'espansione in serie delle funzioni che lo rappresentano troncata
dopo il termine di primo grado. Viene utilizzata in particolare nell'intorno
di un equilibrio dove il comportamento è approssimato da un sistema
lineare la cui matrice A è rappresentata dallo Jacobiano del sistema
originario, valutato per x e u corrispondenti all'equilibrio
stesso. Linearizzazione:
Approssimazione locale del funzionamento di un sistema dinamico,
mediante l'espansione in serie delle funzioni che lo rappresentano troncata
dopo il termine di primo grado. Viene utilizzata in particolare nell'intorno
di un equilibrio dove il comportamento è approssimato da un sistema
lineare la cui matrice A è rappresentata dallo Jacobiano del sistema
originario, valutato per x e u corrispondenti all'equilibrio
stesso. |
 Matrice
definita positiva: Proprietà
di una matrice P verificata se la forma quadratica Matrice
definita positiva: Proprietà
di una matrice P verificata se la forma quadratica 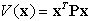 ad essa associata è positiva per tutti i vettori
ad essa associata è positiva per tutti i vettori 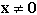 . . |
|
 Matrice
di osservabilità o Matrice di Kalman:
Matrice avente le colonne costituite dai vettori di osservabilità: Matrice
di osservabilità o Matrice di Kalman:
Matrice avente le colonne costituite dai vettori di osservabilità:
O
= | CT ATCT
(AT)2CT ...(AT)n-1CT|
Il campo di
O costituisce il sottospazio di osservabilità.
|
 Matrice
di raggiungibilità o Matrice di Kalman:
Matrice avente le colonne costituite
dai vettori di raggiungibilità: Matrice
di raggiungibilità o Matrice di Kalman:
Matrice avente le colonne costituite
dai vettori di raggiungibilità:
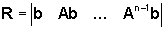
Il campo di
R costituisce il sottospazio di raggiungibilità.
|
 Metodo
di Souriau: Metodo per l'inversione
della matrice (pI-A) di dimensioni Metodo
di Souriau: Metodo per l'inversione
della matrice (pI-A) di dimensioni 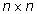 . .
Posta la matrice (pI-A)-1
nella
forma
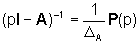 dove P(p) è una matrice
dove P(p) è una matrice 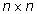 di polinomi di grado minore di n e DA(p)è
il polinomio caratteristico della matrice A, DA(p)
e P(p) si calcolano con le due formule seguenti
di polinomi di grado minore di n e DA(p)è
il polinomio caratteristico della matrice A, DA(p)
e P(p) si calcolano con le due formule seguenti
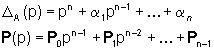 dove
dove
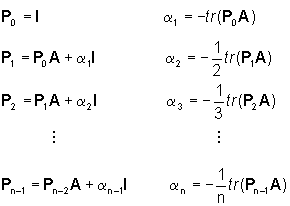
Se, a conti fatti, la funzione di trasferimento
G(p)=n(p)/d(p) ha il polinomio d(p) di grado n, allora dalle
formule di Souriau segue che d(p)=D(p)=DA(p)
cioé il modello ARMA (N(p),D(p)) del sistema è in forma ridotta
ed è, quindi, deducibile dalla funzione di trasferimento. Inoltre,
sempre nel caso di modello ARMA ridotto, i poli della funzione di trasferimento
sono n e coincidono con gli autovalori della matrice
A. Nal
caso, invece, il modello ARMA non sia in forma ridotta, i poli della funzione
di trasferimento sono meno di
n, ma coincidono sempre con alcuni
degli autovalori della matrice
A. |
 Movimento:Soluzione,
x(.) per Movimento:Soluzione,
x(.) per 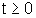 ,
delle equazioni di stato, fissato lo stato iniziale x(0) e l'ingresso
u(t) per ,
delle equazioni di stato, fissato lo stato iniziale x(0) e l'ingresso
u(t) per 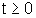 ,
(che tale soluzione sia unica è evidente per i sistemi a tempo
discreto, mentre per i sistemi a tempo continuo è conseguenza di
risultati classici sull'esistenza e unicità della soluzione delle
equazioni differenziali ordinarie). ,
(che tale soluzione sia unica è evidente per i sistemi a tempo
discreto, mentre per i sistemi a tempo continuo è conseguenza di
risultati classici sull'esistenza e unicità della soluzione delle
equazioni differenziali ordinarie). |
 Movimento
libero: Contributo
allo stato del sistema in ogni istante, dipendente unicamente dallo stato
iniziale. Movimento
libero: Contributo
allo stato del sistema in ogni istante, dipendente unicamente dallo stato
iniziale. |
 Movimento
forzato: Contributo
allo stato del sistema in ogni istante, dipendente unicamente dall'ingresso. Movimento
forzato: Contributo
allo stato del sistema in ogni istante, dipendente unicamente dall'ingresso. |
 Ordine
del sistema: Dimensione n del
vettore di stato. Ordine
del sistema: Dimensione n del
vettore di stato. |
 Osservabilità
di un sistema dinamico: Proprietà di un sistema lineare
che determina la possibilità di risolvere il problema "inverso",
cioè quello del calcolo dello stato iniziale x(0) a partire dalla
conoscenza delle funzioni di ingresso e uscita nell'intervallo di tempo
[0,t). Osservabilità
di un sistema dinamico: Proprietà di un sistema lineare
che determina la possibilità di risolvere il problema "inverso",
cioè quello del calcolo dello stato iniziale x(0) a partire dalla
conoscenza delle funzioni di ingresso e uscita nell'intervallo di tempo
[0,t). |
 Poli
della funzione di trasferimento (o del sistema): Gli zeri dei
polinomi lb(.)
(sono gli autovalori della parte raggiungibile
e osservabile). Poli
della funzione di trasferimento (o del sistema): Gli zeri dei
polinomi lb(.)
(sono gli autovalori della parte raggiungibile
e osservabile). |
 Principio
di sovrapposizione: Se alle cause
( Principio
di sovrapposizione: Se alle cause
(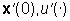 ) corrisponde
l'effetto y'(.) e alle cause ( ) corrisponde
l'effetto y'(.) e alle cause (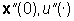 )
corrisponde l'effetto )
corrisponde l'effetto 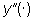 allora, in un sistema lineare, alla combinazione lineare
allora, in un sistema lineare, alla combinazione lineare 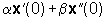 , , 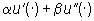 delle cause corrisponde la stessa combinazione lineare
delle cause corrisponde la stessa combinazione lineare 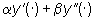 degli effetti.
degli effetti. |
 Problema
della realizzazione: Problema della determinazione
di una quaterna (A,b,cT,d)
che abbia come modello ARMA un modello (N(p),D(p)) assegnato. (Con lo
stesso nome si indica anche la quaterna (A,b, cT,d)
che risolve il problema). La soluzione di questo problema non è
unica, per cui risulta di particolare interesse determinare la realizzazione
di ordine minimo. Problema
della realizzazione: Problema della determinazione
di una quaterna (A,b,cT,d)
che abbia come modello ARMA un modello (N(p),D(p)) assegnato. (Con lo
stesso nome si indica anche la quaterna (A,b, cT,d)
che risolve il problema). La soluzione di questo problema non è
unica, per cui risulta di particolare interesse determinare la realizzazione
di ordine minimo. |
 Ricostruibilità:
Proprietà di un sistema dinamico relativa alla possibilità
di calcolare lo stato finale x(t). Ricostruibilità:
Proprietà di un sistema dinamico relativa alla possibilità
di calcolare lo stato finale x(t). |
 Ricostruttore
dello stato: Copia del sistema (con stato Ricostruttore
dello stato: Copia del sistema (con stato 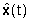 )
cui è applicato, oltre all'ingresso u(t), un secondo ingresso
( )
cui è applicato, oltre all'ingresso u(t), un secondo ingresso
(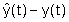 ) legato
alla differenza tra l'uscita ricostruita ) legato
alla differenza tra l'uscita ricostruita 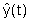 e l'uscita del sistema.
e l'uscita del sistema. |
 Risposta
all'impulso: La
risposta all’impulso di un sistema lineare a tempo continuo è l’uscita
del sistema conseguente all’applicazione di un ingresso impulsivo. Perché
tale uscita sia univocamente individuata, si deve precisare lo stato iniziale
del sistema che, normalmente, viene supposto nullo. Risposta
all'impulso: La
risposta all’impulso di un sistema lineare a tempo continuo è l’uscita
del sistema conseguente all’applicazione di un ingresso impulsivo. Perché
tale uscita sia univocamente individuata, si deve precisare lo stato iniziale
del sistema che, normalmente, viene supposto nullo.
La risposta all’impulso di un sistema continuo
risulta così l’uscita del sistema
con x(0)=0 e u(t)=imp(t).
|
 Risposta
alla rampa: E' l'uscita del sistema con x(0)=0
e u(t)=t Risposta
alla rampa: E' l'uscita del sistema con x(0)=0
e u(t)=t 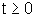 .
Poichè la rampa è l'integrale dello scalino, è immediato
concludere che la risposta alla rampa di un sistema lineare è l'integrale
di quella allo scalino. .
Poichè la rampa è l'integrale dello scalino, è immediato
concludere che la risposta alla rampa di un sistema lineare è l'integrale
di quella allo scalino. |
 Risposta
allo scalino: E' l'uscita del sistema
con x(0)=0 e u(t)=1 Risposta
allo scalino: E' l'uscita del sistema
con x(0)=0 e u(t)=1 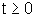 .
Poichè lo scalino è l'integrale dell'impulso è immediato
concludere che la risposta allo scalino di un sistema lineare è
l'integrale della risposta all'impulso. .
Poichè lo scalino è l'integrale dell'impulso è immediato
concludere che la risposta allo scalino di un sistema lineare è
l'integrale della risposta all'impulso. |
 Risposta
in frequenza: Coppia di funzioni Risposta
in frequenza: Coppia di funzioni 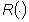 e
e 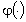 .
R(w) è
l'ampiezza della sinusoide che si ottiene, a transitorio esaurito, come
risposta di un sistema lineare ad una sinusoide di pulsazione w
e ampiezza unitaria e j(w)
è lo sfasamento della stessa rispetto alla precedente. .
R(w) è
l'ampiezza della sinusoide che si ottiene, a transitorio esaurito, come
risposta di un sistema lineare ad una sinusoide di pulsazione w
e ampiezza unitaria e j(w)
è lo sfasamento della stessa rispetto alla precedente.
La risposta in frequenza (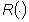 ,
,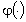 )
dI un sistema lineare a tempo continuo è univocamente individuata
dalla funzione di trasferimento G(s) del sistema. Più precisamente
R(w)
e j(w)
sono, rispettivamente, il modulo e l’argomento del numero complesso G(iw)
cioè G(iw)
= R(w)eij(w) )
dI un sistema lineare a tempo continuo è univocamente individuata
dalla funzione di trasferimento G(s) del sistema. Più precisamente
R(w)
e j(w)
sono, rispettivamente, il modulo e l’argomento del numero complesso G(iw)
cioè G(iw)
= R(w)eij(w) |
 Rivelabilità:
Possibilità di ricostruire, almeno asintoticamente,
lo stato di un sistema per mezzo di un ricostruttore lineare e invariante. Rivelabilità:
Possibilità di ricostruire, almeno asintoticamente,
lo stato di un sistema per mezzo di un ricostruttore lineare e invariante. |
 Sistema
all' equilibrio: Un sistema si
dice all'equilibrio se ingresso e stato (e, quindi, anche uscita, nel
caso di sistemi invarianti) sono costanti, cioè se Sistema
all' equilibrio: Un sistema si
dice all'equilibrio se ingresso e stato (e, quindi, anche uscita, nel
caso di sistemi invarianti) sono costanti, cioè se
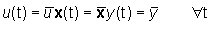 Il vettore
Il vettore 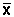 si chiama stato di equilibrio.
si chiama stato di equilibrio. |
 Sistemi
a memoria finita: Sistemi in cui
lo stato iniziale influenza l'evoluzione del sistema soltanto per un periodo
di tempo finito. Nel caso lineare, deve trattarsi necessariamente di sistemi
discreti. Sistemi
a memoria finita: Sistemi in cui
lo stato iniziale influenza l'evoluzione del sistema soltanto per un periodo
di tempo finito. Nel caso lineare, deve trattarsi necessariamente di sistemi
discreti. |
 Sistemi
a sfasamento minimo:
Sistemi
senza zeri o con zeri stabili. Sono sistemi senza ingressi nascosti o
con ingressi nascosti che tendono asintoticamente a zero (con rapidità
legata allo zero "dominante"). Sistemi
a sfasamento minimo:
Sistemi
senza zeri o con zeri stabili. Sono sistemi senza ingressi nascosti o
con ingressi nascosti che tendono asintoticamente a zero (con rapidità
legata allo zero "dominante"). |
 Sistemi
a sfasamento non minimo:
Sistemi
con zeri instabili e, quindi, ingressi nascosti illimitati (o, comunque,
non tendenti a zero). Sistemi
a sfasamento non minimo:
Sistemi
con zeri instabili e, quindi, ingressi nascosti illimitati (o, comunque,
non tendenti a zero). |
 Sistema
asintoticamente stabile: Un
sistema è asintoticamente stabile se e solo se per ogni ingresso Sistema
asintoticamente stabile: Un
sistema è asintoticamente stabile se e solo se per ogni ingresso 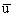 esiste un solo stato di equilibrio
esiste un solo stato di equilibrio 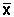 verso cui tende lo stato del sistema per qualsiasi x(0) se
verso cui tende lo stato del sistema per qualsiasi x(0) se 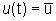 . . |
 Sistemi
autonomi: Sistemi senza ingresso (b=0),
o con ingresso identicamente nullo. Sistemi
autonomi: Sistemi senza ingresso (b=0),
o con ingresso identicamente nullo. |
 Sistema
completamente osservabile:
Sistema nel quale gli n vettori CT,
ATCT, (AT)2CT,
...,(AT)n-1CT,
detti vettori di osservabilità, sono linearmente indipendenti.
In un sistema completamente osservabile, lo stato iniziale può
essere calcolato se le funzioni di ingresso e uscita sono note su un intervallo
di tempo di durata qualsiasi se il sistema è a tempo continuo e
di durata al più pari a n se il sistema
è a tempo discreto. Sistema
completamente osservabile:
Sistema nel quale gli n vettori CT,
ATCT, (AT)2CT,
...,(AT)n-1CT,
detti vettori di osservabilità, sono linearmente indipendenti.
In un sistema completamente osservabile, lo stato iniziale può
essere calcolato se le funzioni di ingresso e uscita sono note su un intervallo
di tempo di durata qualsiasi se il sistema è a tempo continuo e
di durata al più pari a n se il sistema
è a tempo discreto. |
 Sistema
completamente raggiungibile: Sistema
nel quale l'insieme
Xr(t) di tuttti gli stati raggiungibili all'istante t a partire
dall'origine dello spazio di stato
è uguale a Rn. Sistema
completamente raggiungibile: Sistema
nel quale l'insieme
Xr(t) di tuttti gli stati raggiungibili all'istante t a partire
dall'origine dello spazio di stato
è uguale a Rn. |
 Sistema improprio:
Sistema del tipo Sistema improprio:
Sistema del tipo 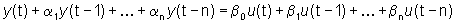 in cui
in cui 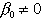 ,
cioè l'ingresso u(t) influenza direttamente l'uscita y(t). ,
cioè l'ingresso u(t) influenza direttamente l'uscita y(t). |
 Sistemi
lineari (definizione interna): Classe
particolare di sistemi dinamici. Essi sono caratterizzati da variabili
di ingresso, stato e uscita, nel seguito indicate
con u, x e y. Con t si indica, invece, il
tempo, che può essere un intero (sistema a tempo discreto)
o un reale (sistema a tempo continuo). Limitandoci al caso dei
sistemi con un solo ingresso e una sola uscita e a dimensioni
finite dobbiamo ulteriormente assumere che Sistemi
lineari (definizione interna): Classe
particolare di sistemi dinamici. Essi sono caratterizzati da variabili
di ingresso, stato e uscita, nel seguito indicate
con u, x e y. Con t si indica, invece, il
tempo, che può essere un intero (sistema a tempo discreto)
o un reale (sistema a tempo continuo). Limitandoci al caso dei
sistemi con un solo ingresso e una sola uscita e a dimensioni
finite dobbiamo ulteriormente assumere che
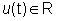 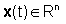 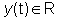
dove la dimensione
n
del vettore di stato si chiama ordine del sistema.
I sistemi lineari
a tempo discreto come quei sistemi in cui lo stato si aggiorna secondo
una equazione lineare, detta equazione di stato,
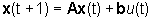 (1)
dove A è una
matrice
(1)
dove A è una
matrice 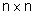 e
b un vettore e
b un vettore 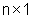 e l'uscita dipende dallo stato e dall'ingresso secondo una equazione lineare,
detta trasformazione d'uscita,
e l'uscita dipende dallo stato e dall'ingresso secondo una equazione lineare,
detta trasformazione d'uscita,
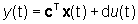 (2)
(2)
dove cT
è un vettore riga 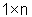 e d un reale. Scritta per ogni componente xi del
vettore di stato, la (1) corrisponde a
e d un reale. Scritta per ogni componente xi del
vettore di stato, la (1) corrisponde a
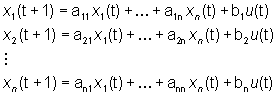 mentre la (2) si specifica
in
mentre la (2) si specifica
in
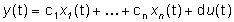
 Sistemi
lineari (definizione esterna): Una
definizione alternativa è quella "esterna", che coinvolge, invece,
soltanto ingresso e uscita. Secondo questa definizione, in un sistema
lineare a tempo discreto di ordine n, una somma pesata degli ultimi
(n+1) valori di ingresso uguaglia, in ogni istante di tempo t, una somma
pesata dei corrispondenti valori di uscita, cioé Sistemi
lineari (definizione esterna): Una
definizione alternativa è quella "esterna", che coinvolge, invece,
soltanto ingresso e uscita. Secondo questa definizione, in un sistema
lineare a tempo discreto di ordine n, una somma pesata degli ultimi
(n+1) valori di ingresso uguaglia, in ogni istante di tempo t, una somma
pesata dei corrispondenti valori di uscita, cioé
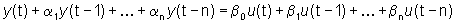
|
 Sistemi
in cascata: Due
sistemi sono collegati in cascata quando l'uscita del primo sistema
è l'ingresso del secondo. Sistemi
in cascata: Due
sistemi sono collegati in cascata quando l'uscita del primo sistema
è l'ingresso del secondo. |
 Sistemi
in parallelo: Due
sistemi sono collegati in parallelo quando hanno l'ingresso in comune
e le loro uscite si sommano. Sistemi
in parallelo: Due
sistemi sono collegati in parallelo quando hanno l'ingresso in comune
e le loro uscite si sommano. |
 Sistemi
in retroazione: Due
sistemi sono collegati in retroazione quando l'ingresso del primo è
la somma di un ingresso Sistemi
in retroazione: Due
sistemi sono collegati in retroazione quando l'ingresso del primo è
la somma di un ingresso
esterno
u e dell'uscita del secondo e l'ingresso del secondo è l'uscita
del primo. |
 Sistema
proprio: Sistema del tipo Sistema
proprio: Sistema del tipo 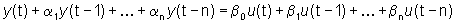 in cui bo=0.
in cui bo=0. |
 Spazio
delle fasi: Lo
spazio di stato si chiama spazio delle fasi quando Spazio
delle fasi: Lo
spazio di stato si chiama spazio delle fasi quando
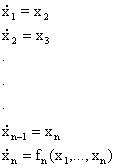
|
 Stabilizzabilità:
Possibilità di trasformare un sistema assegnato (A,b,cT,d)
in un sistema asintoticamente stabile, asservendone l'ingresso allo stato
per mezzo di una legge di controllo lineare. Immaginando che il sistema
sia scomposto nelle sue quattro parti con stato za, zb,
zc e zd, ciò equivale a supporre che Stabilizzabilità:
Possibilità di trasformare un sistema assegnato (A,b,cT,d)
in un sistema asintoticamente stabile, asservendone l'ingresso allo stato
per mezzo di una legge di controllo lineare. Immaginando che il sistema
sia scomposto nelle sue quattro parti con stato za, zb,
zc e zd, ciò equivale a supporre che
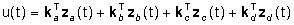
|
 Stabilità
esterna: Un
sistema lineare è esternamente stabile se e solo se la sua uscita
forzata è limitata per ogni ingresso limitato. Stabilità
esterna: Un
sistema lineare è esternamente stabile se e solo se la sua uscita
forzata è limitata per ogni ingresso limitato. |
 Traiettoria
o orbita: Insieme {x(t), Traiettoria
o orbita: Insieme {x(t), 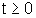 }
nello spazio di stato Rn. }
nello spazio di stato Rn.
-
Nel caso dei sistemi a tempo continuo
la traiettoria è una linea radicata nel punto x(0)
e con un ben preciso verso di percorrenza, quello del tempo.
- Nel caso dei sistemi a tempo discreto la traiettoria
è invece una successione ordinata di punti {x(0),x(1),…}
che, per motivi di chiarezza, è però consuetudine
congiungere con dei segmenti rettilinei orientati.
|
 Trasformata
di Fourier: funzione Trasformata
di Fourier: funzione 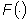 definita:
definita:
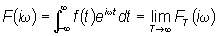
|
 Trasformata
di Laplace: funzione Trasformata
di Laplace: funzione 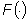 ,
spesso indicata con ,
spesso indicata con 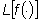 dove
dove
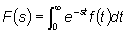 indicata con s la variabile complessa (cioè
s
= s + iw).
indicata con s la variabile complessa (cioè
s
= s + iw).
La trasformata di Fourier è una funzione
complessa definita nel dominio Re(s)
> s0 dove
s0
è
il più piccolo numero reale tale che s
< s0
implich i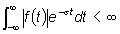 . .
La trasformazione di Laplace 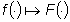 gode di un certo numero di proprietà. Innanzitutto, tale trasformazione
è lineare poichè
gode di un certo numero di proprietà. Innanzitutto, tale trasformazione
è lineare poichè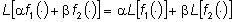 . .
Inoltre, la trasformata di Laplace 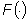 di una qualsiasi funzione
di una qualsiasi funzione 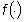 è una funzione analitica nel suo dominio di definizione Re(s)>s0.
è una funzione analitica nel suo dominio di definizione Re(s)>s0. |
 Trasformata Zeta:
la
trasformata Zeta di una funzione Trasformata Zeta:
la
trasformata Zeta di una funzione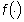 definita in corrispondenza dei numeri interi non negativi, indicata con
definita in corrispondenza dei numeri interi non negativi, indicata con 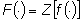 è semplicemente data dalla serie:
è semplicemente data dalla serie:
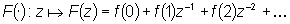
|
 Zeri
della funzione di trasferimento (o del sistema): Gli
zeri dei polinomi Nb(.), numeratore della
funzione di trasferimento o della parte a media mobile del modello ARMA. Zeri
della funzione di trasferimento (o del sistema): Gli
zeri dei polinomi Nb(.), numeratore della
funzione di trasferimento o della parte a media mobile del modello ARMA. |

