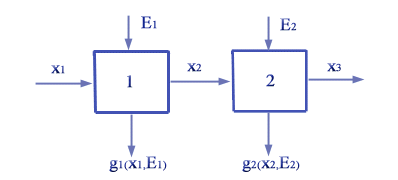
Si consideri il problema (descritto in figura) di due flotte cooperative operanti in cascata sullo stesso stock di pesci, dove E_i indica lo sforzo attuato dalla flotta i, mentre x_j (j=1,2,3) indica la consistenza dello stock prima che venga intercettato rispettivamente dalla prima e dalla seconda flotta e dopo la pesca. Siano inoltre, sempre per la flotta i, q_i il coefficiente di catturabilità, che rappresenta l’efficienza della flotta; c_i il costo per unità di sforzo e p_i il prezzo unitario di vendita del pescato. Si supponga che la dinamica dello stock e il ricavo delle flotte siano descritti dalle seguenti equazioni:

x_i+1 = x_i exp(-q_iE_i)                                    i = 1, 2

g_i(x_i,E_i) =p_i x_i(1 – exp(-q_iE_i )) - c_iE_i                         i = 1, 2

Inoltre si supponga di conoscere la consistenza dello stock prima che venga intercettato (x₁=C) e di volere che alla fine della pesca lo stock residuo sia x₃=N (ovviamente con N<C) .

Si determini la soluzione ottima (E⁰₁, E⁰₂), cioè l’allocazione dello sforzo che massimizza il guadagno complessivo [g₁(x₁,E₁) + g₂(x₂,E₂)].