Si indichino con e x1 x2
rispettivamente le quantità in kg delle sostanze alimentari A e
B somministrate giornalmente a ogni pollo. Il costo giornaliero della dieta
di un pollo è dato da
CAx1 + CBx2³ C (1) PAX1 + PBx2³ P (2) 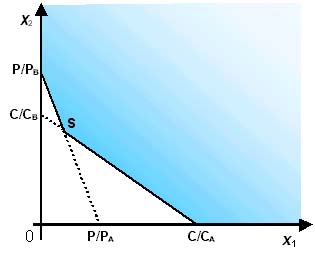
Infine, occorre tener conto dei vincoli di non negatività x1, x2³ 0Per definire la regione delle soluzioni ammissibili, è necessario rappresentare nel piano x1 x2 le due rette, di coefficiente angolare rispettivamente -CA/CB e -PA/PB, che si ottengono considerando le relazioni di uguaglianza nei vincoli (1) e (2). Poiché PB/PA < CB/CA , la retta (2) risulta più inclinata della retta (1). Perché la soluzione ottima possa essere data da una miscela di x1 e x2, occorre che la regione di ammissibilità abbia un punto angoloso all’interno del primo quadrante, cioè che il punto d’intersezione S delle rette (1) e (2) sia nel primo quadrante. Si ricava facilmente dalla figura che la condizione perché ciò avvenga è che siano contemporaneamente verificate le relazioni : P/PB > C/CB e P/PA < C/CA cioèInfine perché la soluzione ottima sia proprio in S, l’inclinazione delle linee di livello della funzione obiettivo deve essere intermedia tra le inclinazioni delle rette (1) e (2), cioè PB/PA < PA/PB < CB/CA . |
