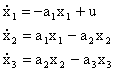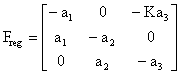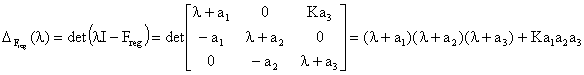Controllo impianto chimico: SOLUZIONE
Indicato con xi(t) il volume di liquido presente nel­l’i-esimo serbatoio (i=1,2,3), le equazioni di stato (bilancio di massa) sono date da:
e la trasformazione di uscita è
La portata di ingresso u(t) dipende però dallo stato del sistema e da altre variabili di ingresso (legge di controllo) nel modo seguente:
Per discutere la sensibilità della variabile z(t) al disturbo d(t) possiamo considerare la situazione di equilibrio conseguente ad una portata d(t) costante e pari a d. In questo caso abbiamo , i = 1, 2, 3 e quindi u = ai xi = y = z - d, per cui dalla(1) si ottiene
z - d = (1+K) Z – K d - K (z - d)
da cui si ricava
Questa relazione mostra che senza la legge di controllo (K = 0) il disturbo d si ripercuote direttamente sulla variabile di interesse (z = Z + d), mentre con la legge di controllo (K>0) si ottiene un’attenuazione del disturbo : se, ad esempio, i1 guadagno della elettrovalvola è unitario il disturbo viene dimezzato . Da questo punto di vista è quindi conveniente orientarsi verso progetti ad elevato guadagno K dell'elettrovalvola.
E’ però importante determinare fino a che punto si può aumentare il guadagno K senza rendere l’intero sistema instabile. Per questo si devono semplicemente determinare gli autovalori del sistema in funzione del parametro K e verificare se la parte reale di questi autovalori è sempre negativa o se essa diventa positiva per valori di K troppo elevati. La matrice del sistema regolato. (si tenga conto della (1)) è data da
per cui si ha
Per semplificare la trattazione che segue supponiamo che i tre serbatoi che costituiscono l’impianto siano uguali cosi che a1 = a2 = a3 = a. In questo caso abbiamo
per cui i tre autovalori sono dati da

 


e sono quindi disposti nel piano complesso sulla circonferenza di centro (-a, 0) e di raggio , come indicato in figura.
 

Perché i tre autovalori abbiamo parte reale negativa è quindi necessario che   sia minore di a e, quindi, che K<8.

La scelta del guadagno K dell'elettrovalvola deve pertanto essere il risultato di un compromesso: più alto è il guadagno (purché minore di 8) più l’uscita è insensibile al disturbo ma più lenti sono i transitori (autovalori più vicini all’asse immaginario).

ESERCIZIO PRECEDENTE
Testo
  ESERCIZIO SUCCESSIVO