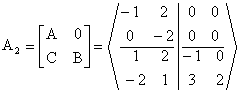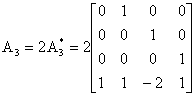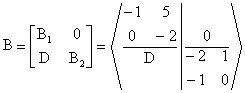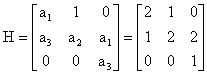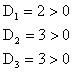La traccia della matrice A₁ è positiva (+ 2) per cui almeno uno dei quattro autovalori di A₁ ha parte reale positiva. Il corrispondente sistema è quindi instabile.

Per la seconda matrice il criterio della traccia non fornisce alcuna informazione. La matrice A₂ può però essere partizionata nel seguente modo

per cui

Gli autovalori di A₂ sono pertanto gli autovalori di A e di B. Ma le matrici A e B sono in forma triangolare, per cui i loro autovalori sono gli elementi sulla diagonale. Poiché uno di questi è positivo (+2) il corrispondente sistema è instabile.

La matrice A₃ sarebbe in forma canonica di controllo se sulla sua pseudodiagonale comparissero elementi unitari anziché pari a 2. In altre parole, possiamo scrivere

e la matrice  è in forma canonica di controllo, per cui gli elementi della sua ultima riga letti da destra verso sinistra e cambiati dl segno sono i coefficienti a₁, …, a₄ del suo polinomio caratteristico.

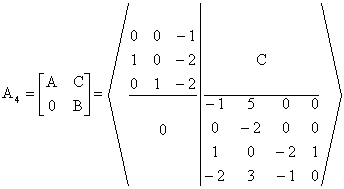
Poiché questi elementi non sono tutti positivi dal criterio di Hurwitz si deduce che i quattro autovalori di  non hanno tutti parte reale negativa. Poiché gli autovalori di A₃ sono doppi di quelli di  ne segue che anche A₃ non ha tutti gli autovalori con parte reale negativa, per cui il corrispondente sistema non è asintoticamente stabile.

La matrice A₄ può essere partizionata nel modo seguente

per cui

Ma la matrice B può a sua volta essere partizionata come segue

per cui  e quindi, in conclusione,

cioè i sette autovalori della matrice A₄ sono i tre autovalori della matrice A, i due autovalori della matrice B₁ e i due autovalori della matrice B₂. Per quanto riguarda la matrice A, che (a parte una trasposizione) è in forma canonica di controllo, possiamo applicare il criterio di Hurwitz

che afferma quindi che i tre autovalori della matrice A hanno parte reale negativa. La matrice B₁ è in forma triangolare per cui i suoi autovalori sano gli elementi della diagonale, che sono negativi (-1 e -2). Infine, gli autovalori della matrice A₃ si calcolano immediatamente. Essendo

gli autovalori di A₃ sono coincidenti e pari a -1.

I sette autovalori di A₄ sono quindi tutti negativi o a parte reale negativa e pertanto il corrispondente sistema lineare è asintoticamente stabile.