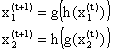|
L’interpretazione
geometrica del metodo iterativo, riportata in figura, mostra chiaramente
che in certi casi il metodo converge mentre in altri diverge.
La condizione di convergenza è molto semplice da ricavare pur di notare che i successivi, valori di x1 e x2 sono legati tra loro dalle relazioni: In
altre parole, tali valori sono lo stato di un sistema dinamico non lineare
che ammette lo stato (
) come stato di equilibrio. Il sistema (1) può essere linearizzato
nell’intorno di tale equilibrio e il suo Jacobiano è dato da:I
due autovalori del sistema linearizzato sono pertanto uguali e pari agli
elementi che compaiono sulla diagonale di J. Pertanto, se
per
il teorema della linearizzazione lo stato di equilibrio
è asintoticamente stabile ed il metodo iterativo converge (pur di
partire da un valore 
sufficientemente vicino a 
). |
