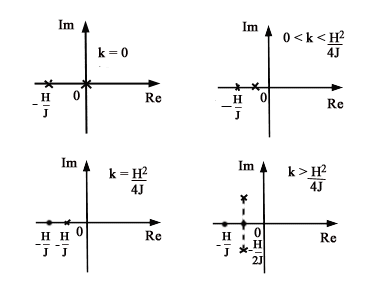soluzione movimento antenna

L'antenna è un sistema del secondo ordine le cui variabili di stato sono

x₁(t) = posizione angolare all’istante t
x₂(t) = velocità angolare all’istante t

Dalla descrizione del problema segue che le equazioni di stato dell’intero sistema sono

dove H è il coefficiente di attrito viscoso (il momento di attrito è proporzionale e opposto alla velocità angolare x₂). Tale sistema è lineare perché del tipo

con

Lo stato di equilibrio corrispondente ad un ingresso v(t) costante

è unico ed è dato da

In altre parole, lo stato di equilibrio è proprio lo stato desiderato (antenna ferma e puntata nella direzione voluta). Affinché il sistema di puntamento sia tecnicamente accettabile è quindi innanzitutto necessario che il sistema sia asintoticamente stabile, perché ciò garantisce che lo stato di equilibrio desiderato sia asintoticamente raggiunto da qualsiasi posizione e velocità si parta. Perché questa proprietà sia verificata, gli autovalori della matrice A devono avere parte reale negativa.

Il polinomio caratteristico di A è dato da

per cui gli autovalori (radici di

)sono

_{Gli
autovalori del sistema hanno quindi parte reale negativa per qualsiasi
valore (positivo) di K ma variano (nel piano complesso) al variare del
parametro di progetto K come mostrato in figura.}

I transitori della variabile x₁(t) per v(t) = v sono quindi del tipo

con Re(l₁)<0 e Re(l₂)<0 per cui x₁(t) tende a v per t che tende all'infinito. Le costanti F e G dipendono dalle condizioni iniziali x₁(0) e x₂(0), ma la rapidità del transitori è comunque legata agli autovalori l₁ e l₂. Nel caso in cui gli autovalori sono reali

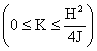la (1) si. può scrivere nella forma

dove T₁ e T₂ sono le “costanti di tempo”

T₁ = -1/l₁ T₂ = -1/l₂

Nel caso invece in cui gli autovalori sono complessi

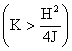posto

la (1) si può scrivere nella forma

dove le costanti L e M dipendono dalle condizioni iniziali x₁(0) e x₂(0). Anche in questo caso, comunque, la “rapidità” del transitorio, individuata dalla costante di tempo T è determinata dalla parte reale dell’autovalore. In conclusione, quindi, per avere transitori rapidi si deve massimizzare la distanza degli autovalori dell’asse immaginario. La soluzione migliore è per tanto quella corrispondente a

. Infatti, se

una delle due costanti di tempo è maggiore di

Quanto detto si può anche visualizzare nel piano di stato (x₁, x₂) in cui si possono tracciare le traiettorie corrispondenti ad ingresso costante v(t) = v. Come già detto, per K>0 in tale piano esiste un unico stato di equilibrio asintoticamente stabile. Tale equilibrio è un nodo stabile per

ed un fuoco stabile per

come mostrato in figura.

Le due traiettorie rettilinee che caratterizzano il nodo stabile ai possono ottenere determinando gli autovettori x⁽¹⁾ e x⁽²⁾ associati ai due autovalori l₁, l₂cioè determinando una soluzione non nulla dell’equazione:

Nel caso limite

i due autovalori ed i due autovettori diventano coincidenti (nodo stabile degenere) ed il quadro delle traiettorie è, pertanto, il seguente:

Tipiche traiettorie nel caso

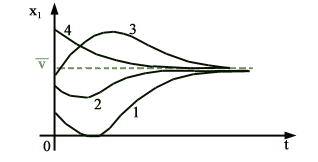
I corrispondenti transitori della variabile x₁(t) sono quindi del tipo indicato in figura:

Sono, pertanto, possibili delle “sovraelongazioni” come nel caso del transitorio n.3: tali sovraelongazioni sono dovute ad una elevata velocità iniziale, che fa si che la posizione di equilibrio v venga raggiunta e addirittura superata nella fase Iniziale del transitorio. Queste sovraelongazioni non vanno tuttavia confuse con le oscillazioni smorzate che si presentano nel caso del fuoco stabile .

In conclusione, il parametro di progetto K può essere fissato pari ad , perché così facendo si ottengono i transitori più rapidi possibili. In tali condizioni, pur esistendo la possibilità di sovraelongazioni vengono certamente evitati fenomeni di tipo oscillatorio. Peraltro, ipotizzando che 1’antenna sia sempre ferma all’istante iniziale, non si hanno sovraelongazioni e i transitori di x₁(t) sono sempre monotoni. Poiché l’angolo desiderato è per forza compreso tra ne segue che il motore da usare deve poter esercitare una coppia massima pari a .