Preda-predatore : SOLUZIONE
In assenza di predatori (x2(t)=0) la preda evolve secondo l’equazione:
che ammette due equilibri
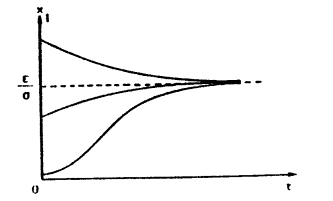
Il primo di questi equilibri è instabile perché l’autovalore del corrispondente sistema linearizzato è positivo (e) mentre il secondo è asintoticamente stabile perché l’autovalore del sistema linearizzato è negativo (-e). La dinamica della preda è, pertanto, del tipo indicato in figura: tutti i movimenti con x1(0) > 0 tendono asintoticamente alla “capacità portante” .

In assenza di prede (x1(t)=0) i predatori invece si estinguono esponenzialmente perché soddisfano l’equazione:

che ammette l’unico stato di equilibrio .
Supponendo, ora, che prede e predatori possano coesistere, imponiamo l’equilibrio ponendo 
Dalle equazioni di stato ricaviamo allora:
Perché tale soluzione abbia significato è necessario che le due componenti dello stato di equilibrio siano positive. Pertanto, la relazione
è la condizione di esistenza di un equilibrio tra prede e predatori. Poiché è la capacità portante delle prede, e è la densità delle prede all’equilibrio (1), la condizione (2) dice che in presenza di predatori le prede sono (all'equilibrio) in numero minore che in assenza di predatori.
Per determinare se lo stato di equilibrio (1) è asintoticamente stabile possiamo calcolare gli autovalori della matrice del sistema linearizzato:
 che ha la seguente equazione caratteristica:
La condizione (2) di esistenza dell’equilibrio implica quindi che gli autovalori del sistema linearizzato abbiano somma negativa e prodotto positivo .
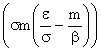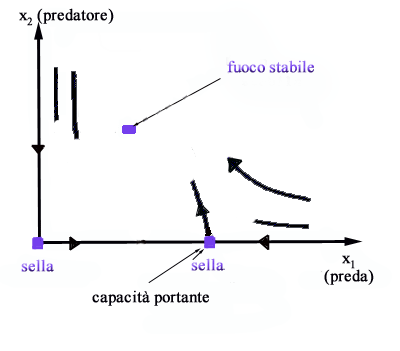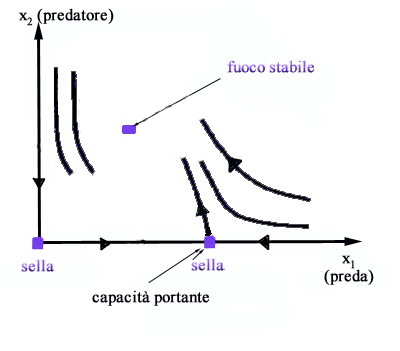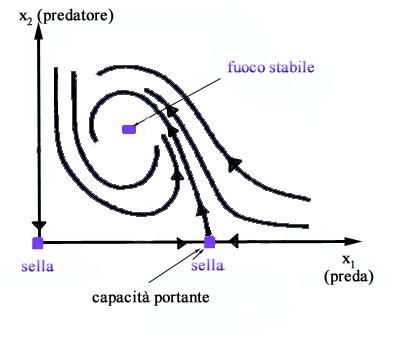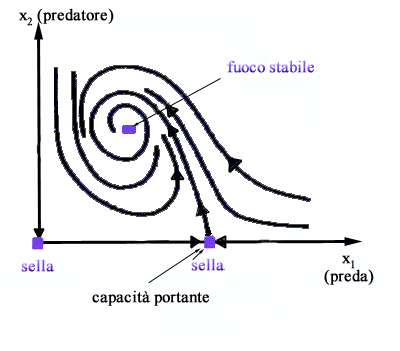
L’equilibrio è pertanto sempre asintoticamente stabile (in effetti tale equilibrio può essere un fuoco stabile o un nodo stabile a seconda del valore dei parametri).
Quanto detto si può riassumere con il seguente quadro delle traiettorie caratterizzato da due selle e da un fuoco stabile.
ESERCIZIO PRECEDENTE
Testo
  ESERCIZIO SUCCESSIVO