|
(a)
Determinazione del tempo minimo
In base alla lunghezza e alla velocità media della categoria di appartenenza, è possibile calcolare per ogni arco il tempo di percorrenza tij espresso in minuti (Fig. 3).
Siano: t(j) = tempo per andare dal nodo A al nodo j (da minimizzare); L’algoritmo
va inizializzato ponendo:
t(A) = 0; G = {A}; k = A; t(j) = ¥ (" j¹A) Per
ogni iterazione vengono poi compiuti i seguenti passi:
(1) aggiornamento dei tempi di percorso: "jÏG : t(j) = min (t(j), t(k) + tkj). (2)
etichettatura di un nodo (viene etichettato il nodo per il quale
il tempo t(j) calcolato al passo (1) è minimo):
sia i : t(i) = min t(j) ; si pone: iÎG ; p(i) = h con hÎG e tale che t(i) = t(h) + thi. (3)
passaggio all’iterazione successiva:
se tutti i nodi sono etichettati: stop; altrimenti: k=i; go to 1. Nel caso in esame si ha: inizializzazione: t(A) = 0; G = A; t(j) = ¥ (j=B,C,D,E,F,G). prima
iterazione:
(1) t(B) = 50; t(C) = 60; t(D) = 150; t(j) = ¥ (j=E,F,G). (2) i = B; G = {A,B}; p(B) = A. (3) k = B; GO TO (1). seconda iterazione: (1) t(C) = 60; t(D) = 130; t(E) = 150; t(j) = ¥ (j=F,G). (2) i = C; G={A,B,C}; p(C) = A. (3) k = C; GO TO (1). terza iterazione: (1) t(D) = 130; t(E) = 150; t(F) = 100; t(j) = ¥ (j=G). (2) i = F; G = {A,B,C,F}; p(F) = C. (3) k = F; GO TO (1). quarta iterazione: (1) t(D) = 130; t(E) = 150; t(G) = 200. (2) i = D; G = {A,B,C,F,D}; p(D) = B. (3) k = D; GO TO (1). quinta iterazione: (1) t(E) = 150; t(G) = 190. (2) i = E; G = {A,B,C,F,D,E}; p(E) = B. (3) k = E; GO TO (1). sesta iterazione: (1) t(G) = 180. (2) i = G; G = {A,B,C,F,D,E,G}; p(G) = E. (3) STOP. E’ ora possibile ricostruire, attraverso la lettura a ritroso dei p(j), il cammino ottimo da A a G: A-B-E-G, per un tempo complessivo di 180 minuti. In Fig. 4 sono indicate le etichette relative ai singoli nodi e, in grassetto, il cammino ottimo da A a G. Si noti che è possibile, senza ulteriori calcoli, ricostruire anche il cammino ottimo tra A e qualunque altro nodo della rete etichettato prima di G.
(b) Determinazione del flusso massimo Il problema è quello di determinare il massimo flusso istradabile dall’origine A alla destinazione G, tenendo conto dell’orientamento e della capacità dei singoli archi. Il problema può essere risolto con un metodo intuitivo, basato sull’ottimizzazione combinatoria. L’idea base del metodo è che il massimo flusso nella rete sarà determinato da una strozzatura (un “collo di bottiglia”) localizzata in qualche punto, per il momento ignoto: qualora fosse possibile individuarlo, si troverebbe la soluzione ottima, in quanto la capacità della strozzatura coinciderà col flusso massimo. Date le seguenti definizioni: taglio: una partizione in due sottoinsiemi (PO e PD) dei nodi della rete, tale che l’origine e la destinazione appartengano a sottoinsiemi diversi; capacità di un taglio: la somma delle capacità degli archi che vanno dal sottoinsieme contenente l’origine (PO) a quello contenente la destinazione (PD); la soluzione ottima è il massimo flusso che può attraversare il taglio con capacità minima. Il
metodo di risoluzione consiste allora nel listare tutti i tagli della rete
(nel caso in esame 25=32), nel verificarne l’ammissibilità
(sia PO che PD devono essere connessi) e, nel caso
di quelli ammissibili, nel calcolarne il taglio. Quest’operazione è
mostrata nella seguente tabella, dove 0 indica l’appartenenza di un nodo
all’insieme P0, 1 indica l’appartenenza di un nodo all’insieme
PD, n.a. indica la non ammissibilità di un taglio.
Dalla tabella risulta che il taglio ottimo è PO = {A}; PD = {B,C,D,E,F,G} con capacità pari a 100, che costituisce il massimo flusso che si può istradare da A a G. Si noti che il problema poteva essere formulato come un programma lineare. Infatti, indicando con xij il flusso di auto sull’arco da i a j e con cij la capacità dell’arco da i a j, il problema della determinazione del flusso massimo da A a G è il seguente: max j = å xAj (1) å xik = å xkj ("k¹A,G) (2) 0 £ xij£ cij (" i,j) (3) La funzione (1) esprime l’obiettivo di massimizzare il numero di auto in partenza dall’origine A; l’insieme dei 5 vincoli (2), uno per nodo con l’esclusione dell’origine A e della destinazione G, esprime l’ipotesi che non vi sia accumulo o dispersione di auto nei nodi della rete; l’insieme dei 16 vincoli e delle 16 condizioni di non negatività (3) esprime le condizioni di funzionamento del sistema, per cui il flusso su ogni arco deve essere non negativo e non superiore alla capacità dell’arco stesso. Il problema così formulato può essere risolto con l’algoritmo del simplesso. |
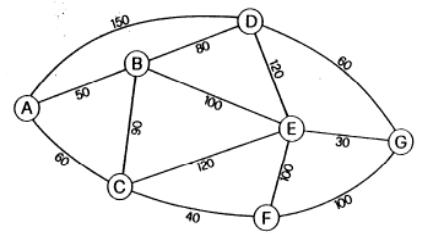 figura
3
figura
3 figura 4
figura 4