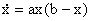
è del tipo 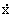=f(x) e rappresenta quindi un sistema dinamico (senza ingresso). Ponendo f(x) = 0 si ottengono due stati dl equilibrio:

  e .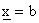

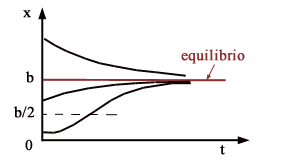
Se 0 < x(t) < b si ha 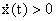  e quindi x(t) aumenta e tende a b. Se, invece, x(t) > b si ha  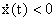 e x(t) diminuisce e tende a b. Lo stato di equilibrio  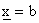 viene quindi asintoticamente raggiunto da qualsiasi stato iniziale x(0) si parta (purché x(0) > 0) (vedi figura). 

I movimenti riportati in figura corrispondono al comportamento reale di sistemi di questo tipo. Essi mostrano come un territorio finito non possa essere sede di un numero illimitato di animali (per questo il parametro b si chiama “capacità portante”) e che la crescita (movimento più basso di figura) avviene secondo le tipica curva a sigmoide. La densità a cui è massimo il tasso di crescita b/2, poiché la funzione f(x) è una parabola con massimo appunto in b/2 (vedi ancora la figura).

Nel caso le trote vengano pescate, possiamo immaginare che il tasso di rimozione h(t) sia proporzionale al numero u(t) di pescatori e alla densità x(t) di trote presenti, cioè

h(t) = k u(t) x(t)

Se il numero di pescatori è costante e pari ad 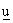  si ottiene l’equazione

che mostra come la presenza del pescatori sia equivalente ad una diminuzione della capacità portante che diventa  _. 

Tra tutti i possibili equilibri quello a massima cattura è pertanto quello corrispondente ad un numero ai pescatori pari ad poiché la cattura   è funzione parabolica di   con massimo appunto in 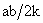  (vedi figura). 

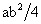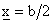All’equilibrio il tasso di cattura è pari ad   ed uguaglia pertanto il massimo tasso di crescita. Consistentemente, la densità di equilibrio che si ottiene in  queste condizioni è   cioè metà della capacità portante. In altre parole il modello afferma che se si vuol sfruttare al massima il lago si deve fissare il numero di pescatori in modo che la densità di trote sia (a regime) la metà che in condizioni naturali.