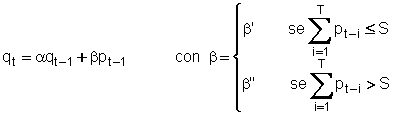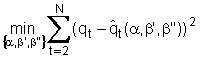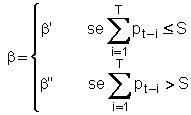|
E’ stato proposto un modello matematico delle portate di piena di un fiume. Detta qt la portata media del giorno t, pt-1 la pioggia nel bacino imbrifero nel giorno precedente ed S un valore limite dello stato di imbibizione del suolo, il modello può essere scritto nel modo seguente: La
struttura del modello può essere facilmente giustificata nel modo
seguente. Se le piogge totali dei T giorni precedenti
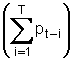non sono state molto elevate (diciamo sono inferiori ad S) il terreno e
la vegetazione continuano ad assorbire parte della pioggia, mentre se il
suolo è già saturo di acqua (piogge dei T giorni precedenti
superiori ad S) gran parte della pioggia scorre in superficie. Sarà
quindi in generale b'' >b'.Volendo
ora adattare questo modello ad un fiume specifico è necessario tarare
i parametri a, b', e b''
e per fare ciò si decide di utilizzare il metodo dei minimi quadrati.
Noti N valori di portata qt e di pioggia pt, t =
1,...,N e T valori precedenti di pioggia, si risolve quindi il seguente
problema di ottimizzazione, le cui variabili di decisione sono i parametria, b',
e b'',
coi
vincoli (t=2,….,N)
dove
Si
dica con quale algoritmo di ottimizzazione è possibile risolvere
questo problema di programmazione matematica.
|
