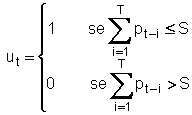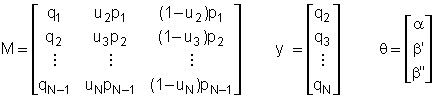| Il
problema è chiaramente di tipo non lineare dato che nella funzione
obiettivo compare un quadrato ed è presente una discontinuità
nei valori di b. Poiché le dimensioni del problema non sono rilevanti
(3 variabili di decisione rappresentate dai parametri da stimare) è
senz’altro possibile utilizzare uno dei più semplici metodi di ricerca
multidimensionale (pattern search, ricerca casuale, ecc.).
Tuttavia è possibile e conveniente riformulare il problema in modo da rendere lineari i vincoli, così da poter utilizzare metodi più efficaci (quali la programmazione quadratica che prevede appunto una funzione obiettivo quadratica con vincoli lineari) o addirittura la formula esplicita per la stima ai minimi quadrati, che può essere applicata appunto a modelli lineari nei parametri. Per linearizzare il vincolo si può procedere nel modo seguente: - si calcola il termine ut a partire dai dati pt nel modo seguente: - si riscrivono i vincoli (t=2,...,N) che è una formula lineare nelle variabili di decisione a, b', b" e consente quindi l’adozione degli aligoritmi di cui si è detto. Posto
infatti
e
indicata con MT la trasposta della matrice M, il valore ottimo
q del vettore dei parametri si determina con la formula
q = (MT M)-1 MT y . |