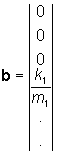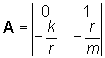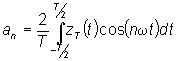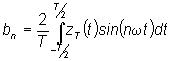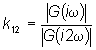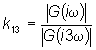IL MODELLO
Il sistema può essere schematizzato come in Fig. 2, dove con x₁(t), x₂(t) e x₃(t) si sono indicate le posizioni delle masse m₁, m₂ e m₃=280[kg] in cui si sono idealmente immaginati concentrati gli assi, la cassa e i passeggeri. Le posizioni x_i(t) sono misurate rispetto a un riferimento fisso (fondo stradale perfettamente liscio) e u(t) rappresenta il livello reale del fondo stradale (misurato rispetto allo stesso riferimento).
 

Fig.2: Il modello dell'autoveicolo

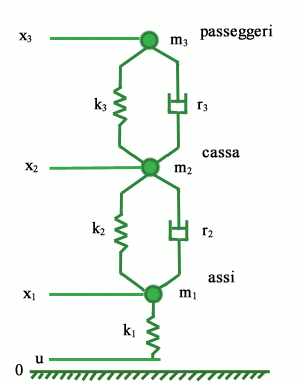
In Fig.2,  k₁, k₂e k₃ rappresentano i coefficienti elastici di pneumatici, sospensioni e cuscini, mentre r₂ e r₃ rappresentano i coefficienti di smorzamento viscoso di smorzatori e cuscini (il coefficiente r₁ di smorzamento dei pneumatici è stato ritenuto trascurabile). Il modello di Fig.2 è un sistema dinamico lineare del sesto ordine. Le prime tre equazioni di stato sono una banale conseguenza della definizione delle variabili

 

mentre le altre tre sono ottenibili scrivendo per ogni massa m_i la legge di Newton (massa X accelerazione = somma delle forze applicate). Ad esempio, tenendo conto che una molla con estensione minore della sua estensione a riposo funziona da respingente, per la massa m₁ (assi) si ottiene:

dove L₁=D/2 è la estensione a riposo dei pneumatici. Analogamente si procede per le equazioni di stato  e  (la cui scrittura è lasciata al lettore come utile esercizio).
 

La dinamica delle variazioni dx₁, dx₂, …, dx₆ rispetto all'equilibrio corrispondente a u=0 è quindi descritta dal sistema lineare:
 

dove la matrice A e il vettore b sono immediatamente ricavabili dalle equazioni di stato tralasciando i termini costanti. Pertanto:
 

(1)

La trasformazione di uscita dy=c^Tdxdeve naturalmente essere definita in funzione della domanda cui si vuole rispondere. Pertanto, per rispondere alla prima domanda, riguardante le vibrazioni della cassa, dovrà essere dy=dx₂ e cioè:

(2')

mentre per rispondere alla seconda domanda, riguardante le vibrazioni dei passeggeri rispetto alla cassa, dovrà essere dy=dx₂ e cioè:
 

(2")

Consideriamo, a titolo di esempio, la prima prova statica,quella effettuata sui pneumatici. In assenza di passeggeri e all'equilibrio la (1) si semplifica (perchè ) e diventa:
 

D'altra parte anche la cassa è in equilibrio e, quindi, la forza elastica  uguaglia il peso m₂g della cassa. Pertanto,
 

da cui si ricava:
 

Analogamente si può procedere per le altre due prove statiche che permettono di determinare k₂ e k₃.

Per quanto riguarda le prove dinamiche, che permettono di ricavare i coefficienti di smorzamento viscoso r in funzione dei coefficienti elastici k, val la pena notare che la frequenza f[Hz] è legata alla pulsazione w[rad/sec] dalla formula:
 

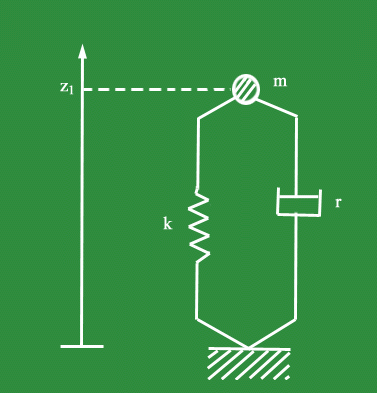
e che la pulsazione w delle oscillazioni di un sistema meccanico del tipo mostrato in Fig.3 coincide con la parte immaginaria degli autovalori  del sistema.
 

Fig. 3: Sistema meccanico massa-molla-smorzatore

Poichè le equazioni del sistema sono:
 

la matrice A del sistema lineare che descrive le variazioni dz₁ e dz₂ rispetto all'equilibrio , è:
 

Gli autovalori di questa matrice sono le radici di:
 

e cioè:
 

Dalla (3) si ottiene allora:
 

che risolta rispetto a r fornisce:
 

MASSIMA VIBRAZIONE DELLA CASSA:

Per rispondere alla prima domanda, cioè per determinare la frequenza f* di sollecitazione trasmessa dal profilo stradale che dà luogo alla massima vibrazione della cassa, è sufficiente determinare la pulsazione di risonanza del sistema (1, 2'), cioè la pulsazione w*=2pf* per cui :
 

La determinazione di tale massimo è ovviamente facilitata qualora si disponga di un package per il tracciamento dei diagrammi di Bode.

ANALISI DELLE ARMONICHE
Una macchina che viaggia sul pavè di lunghezza L a velocità v è soggeta a un treno di impulsi intervallati di un tempo T=L/v. Il treno di impulsi può essere sviluppato, come qualsiasi funzione z_T(t), periodica di periodo T, in serie di Fourier:
 

dove:
 

Nel caso in esame:

a0=1/T

an=2/T

bn=0

per cui:
 

e la prima armonica (o armonica fondamentale) ha la stessa ampiezza di tutte le successive armoniche. Il rapporto K₁₂ (K₁₃) tra le ampiezze della prima e della seconda (terza) armonica delle vibrazioni dei passeggeri rispetto alla cassa è allora dato da:
 

dove G è la funzione di trasferimento del sistema (1, 2"), cioè:
 

con A, b e cT come in (1) e (2").

Se i rapporti K₁₂ e K₁₃ sono espressi in decibel si ha: 
 

Ovviamente la soluzione del problema è facilitata qualora si disponga di un package per il calcolo della risposta in frequenza.

---