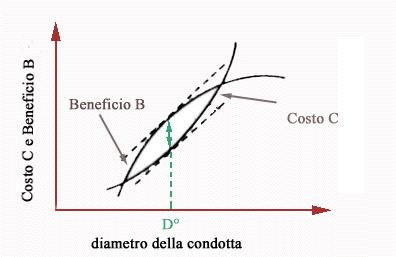
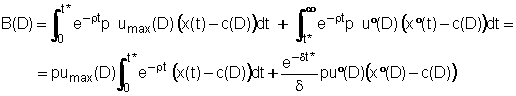Il beneficio B è certamente crescente con il diametro della condotta perché all’aumentare di D aumenta la portata massima umax di alimentazione dell’impianto e diminuiscono le perdite dovute all’attrito. Tuttavia, questi vantaggi tendono a diventare marginali all’aumentare del diametro della condotta per cui ci si può aspettare a priori che la funzione B(D) risulti crescente e concava come mostrato in Fig. 2.
Il valore ottimo D° del diametro è quello per cui è massimo il beneficio netto, cioè la differenza B(D) - C(D) tra benefici e costi, e ciò accade quando il beneficio marginale B' uguaglia il costo marginale C'. Per
determinare il diametro ottimo D° è quindi necessario valutare,
almeno per punti, la funzione beneficio B(D). Ciò non è assolutamente
semplice. Innanzitutto, mentre i costi sono concentrati nel tempo, i benefici
sono distribuiti su tutta la vita dell’impianto, per cui è importante,
per effettuare correttamente il confronto tra costi e benefici, trovare
un metodo di “attualizzazione” dei benefici. Il metodo suggerito dalla
teoria economica è quello dello sconto dei benefici futuri. In altre
parole, se E(t) è la quantità di energia elettrica prodotta
all’istante di tempo t, possiamo supporre che il beneficio attualizzato b
sia dato da
dove r
è il tasso di interesse supposto costante, p(t) é il prezzo
dell’energia e T è la durata prevista dell’impianto. Questa relazione
può essere ulteriormente specificata supponendo che la durata dell’impianto
sia praticamente infinita e che il prezzo dell’energia cresca esponenzialmente
nel tempo
p(t) = p evt Definendo
allora il tasso di interesse deinflazionato d
come la differenza tra p e v,
d = p - v possiamo
dare al beneficio b
la seguente forma
Fissato
il diametro D della condotta, il beneficio B(D) è pertanto il massimo
beneficio b
che si riesca a realizzare
Ciò
significa che B(D) può essere calcolato risolvendo il seguente problema
di controllo ottimo
in
cui l’energia è il prodotto della portata u per il salto x diminuito
delle perdite c, che dipendono dal diametro della condotta (in realtà
le perdite sono funzione anche della portata u(t), ma si è qui fatta
l’ipotesi di considerare un campo di valori di portata abbastanza ristretto
in modo da poter trascurare questa dipendenza).
In
tale funzione la portata u(t) deve soddisfare il vincolo
0 £ u(t) £ umax(D) (2) e
il salto x(t) deve soddisfare il vincolo differenziale
dV(t)/dt = a(t) + u(t) - e(t) in
cui a(t) è la portata degli immissari (in pratica il fiume
Giordano), e(t) è la
portata di evaporazione e V(t) è l’invaso del Mar Morto. Se teniamo
conto della relazione che lega l’invaso V al salto x e del fatto che la
portata di evaporazione è proporzionale secondo un coefficiente a
alla superficie S(x) dello specchio d’acqua, l’equazione differenziale
diventa
dV/dt = dV/dx dx/dt = a + u - a S per
cui può essere messa nella forma classica x = f(x,u)
In
questa equazione V'(x) è negativo, S(x) è decrescente
con x e l’afflusso a può essere per semplicità, considerato
costante. Il livello iniziale x(0) è il livello naturale xn
del Mar Morto che è quello per cui l’evaporazione aS(xn)
è uguale all’afflusso a del Giordano.
Per
risolvere il problema di controllo ottimo (1-3) definiamo la funzione hamiltoniana
e
notiamo che questa funzione è lineare nella variabile di controllo
u. Per questo motivo la massimizzazione dell’hamiltoniano fornisce la seguente
regola
dove s(t) = e-dt p (x – c) +l/V' La
condizione di esistenza di un arco singolare è pertanto
e-dt p (x – c) + l/V' = 0 da
cui segue
l = - p V' (x – c) e-dt e
derivando rispetto al tempo
D’altra
parte per il principio del massimo, deve essere
che
uguagliata con l’espressione precedente (tenendo conto che x è dato
dalla (3) ) fornisce
a - aS(x) - a (x - c) S'(x) = d (x - c) V'(x) (4) che
è la condizione di singolarità. La (4) è un’ equazione
in un’unica incognita: il salto x. Ciò significa che se esistono
archi singolari, questi sono costituiti da stati di equilibrio. La (4)
ammette in generale un’unica soluzione x° data da (vedi (3))
u° = a S(x°) - a La
relazione (4) di singolarità dimostra che il valore di equilibrio
x0 del salto dipende dal tasso di interesse d,
cioè x0 = x0(d). Derivando la
(4) rispetto a d si ottiene
da
cui risulta
Nel
caso specifico della depressione del Mar Morto la superficie S dipende
linearmente da x per cui S" = 0 e il tasso di interesse è
molto piccolo (la Banca Mondiale ha suggerito un valore pari a 0.04) così
che
per
cui all’aumentare del tasso di interesse (che è comunque un parametro
di progetto) si ottengono salti x° sempre più piccoli.
In
conclusione, la gestione ottimale del sistema consiste nell’alimentare
l’impianto con la massima portata possibile umax fin tanto che
in un certo istante t* il salto x, che inizialmente
è pari a xn raggiunge il valore x° (vedi Fig.
3). A questo punto la portata in condotta viene ridotta al valore
u0 = a S(x°) - a, cui viene in seguito
mantenuta.
Se
invece per qualche motivo fortuito (ad esempio un’annata di afflussi notevolmente
elevati) il salto diventa inferiore al valore x°, la regola
di gestione ottima suggerisce di interrompere la produzione di energia
elettrica (u = 0) fin tanto che il salto x° viene ripristinato.
Una volta che si sia determinato il valore ottimo x°(D)
del salto e il corrispondente valore u°(D), si può risolvere
numericamente l’equazione differenziale (3) con u = umax(D)
e x(0) = xn finché ad un certo istante t*
si ha x(t*) = x°(D). Si può così
determinare B(D) con la formula (vedi equazione (1))
in
cui il termine c(D) che rappresenta le perdite è decrescente con
D. Ripetendo questa operazione per vari valori di D si può così
determinare per punti la funzione B(D) che, come detto all’inizio, è
necessaria per eseguire il progetto ottimale dell’intero sistema. Questi
calcoli, eseguiti per il caso specifico del Mar Morto, hanno portato ad
una soluzione ottima caratterizzata da una condotta di diametro
D° di 4,90 m, daun salto x°
di393 m e da unaportata
u° di 285 m3/sec, cui corrisponde un beneficio netto attualizzato
(differenza tra beneficio B(D°) e costo C(D°) ) di 144 milioni
di dollari.

|