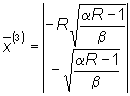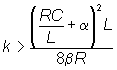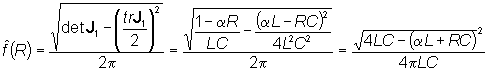dove  è la parte immaginaria degli autovalori dello Jacobiano calcolato nell'equilibrio instabile contenuto all'interno del ciclo.

EQUAZIONI DI STATO: 
Le equazioni di stato di una rete elettrica sono immediatamente ricavabili dalla legge dell'induttore:
 

[tensione sull'induttore]

e dalla legge del condensatore:
 

[corrente nel condensatore]

Nel caso specifico, tenendo conto della caratteristica del BNL, si ottiene:
 
 

	(1)
	(2)

Le (1,2) rappresentano un sistema non lineare del secondo ordine.

EQUILIBRI E CICLI :
E' immediato constatare che il sistema (1,2) con  ammette sempre la soluzione
 

e che per aR>1si hanno anche altri due stati di equilibrio:
 

Lo Jacobiano è dato da:
 

e, pertanto, nell'equilibrio(l'origine dello spazio di stato) si ha:
 

Poichè:
 

segue che traccia e determinante dello Jacobiano sono positivi per 
 

(3)

Poichè aR<1 quando la (3) è verificata, si può concludere che per R<R* il sistema ha un unico equilibrio (l'origine dello spazio di stato) e che tale equilibrio è un repulsore (fuoco instabile o nodo instabile).
E' pertanto lecito pensare che attorno a questo equilibrio esista un ciclo limite stabile G, come mostrato in Fig.2.
 

Fig. 2: Andamento qualitativo delle traiettorie per R<R* (vedi equazione (3)  del testo)

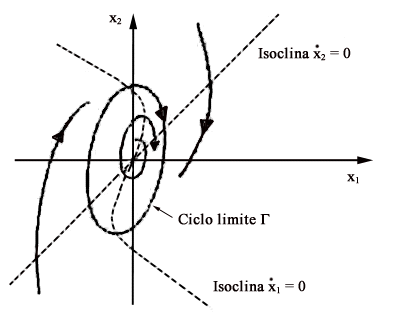
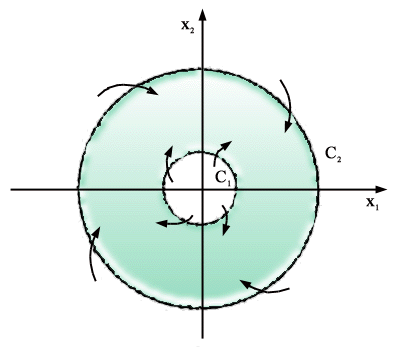
La dimostrazione dell'esistenza del ciclo G si può fare usando il criterio di Poincarè che afferma (vedi Fig.3) che esiste un ciclo stabile in una corona delimitata da due linee chiuse C₁ e C₂ se tali linee sono attraversate dalle traiettorie dall'esterno verso l'interno e se nella corona non esistono stati di equilibrio.
Nel caso del sistema (1,2) con R<R*, l'origine dello spazio di stato è un repulsore e pertanto esiste certamente una linea chiusa C₁ intorno all'origine attraversata dalle traiettorie nel modo indicato in Fig.3.
 

Fig.3: Illustrazione del criterio di Poincarè: se nella corona circolare non esistono  equilibri, allora esiste un ciclo limite

D'altra parte, per R<R*, l'origine è l'unico stato di equilibrio per cui la corona di Fig.3 non contiene equilibri qualsiasi sia la linea C₂. Infine, per dimostrare che esiste una linea chiusa C₂ attraversata dalle traiettorie nel modo indicato in Fig.3 si può considerare come linea C₂ una linea di livello
 

v(x) = k

della funzione energia
 

e verificare che per valori di k sufficientemente elevati  sull'ellisse V(x)=k. Infatti:
 

e poichè sulla linea C₂
 

risulta:
 

La funzione  è mostrata in Fig.4 dove:
 

Pertanto se , cioè se
 

(4)

è negativa su tutta la linea C₂ corrispondente a V=k.
 

Fig. 4: Andamento della funzione Y(x2)

E' interessante notare che la discussione fatta sul segno di  può essere interpretata dal punto di vista energetico perchè il termine  che compare in  rappresenta la potenza dissipata nel resistore, mentre il termine  rappresenta la potenza scambiata dal bipolo non lineare col resto del circuito. Affermare che  è negativo sulla linea C₂ individuata da V=k con k che soddisfa la (4) è allora equivalente ad affermare che su C₂ la potenza dissipata nel resistore è maggiore della potenza eventualmente immessa nel circuito dal BNL.

Per dimostrare che il quadro delle traiettorie è effettivamente quello mostrato in Fig.2 andrebbe ancora dimostrato che il ciclo G è unico. Tale dimostrazione è tutt'altro che semplice e viene pertanto omessa.
 

FREQUENZA  DI OSCILLAZIONE:
Per determinare la frequenza di oscillazione f(R) corrispondente ad ogni valore di R<R* si può usare un package di simulazione (attenzione alla scelta dell'unità di tempo) e determinare così il periodo T(R) del ciclo G(R). 
Ovviamente, f(R)=1/T(R).

Il risultato così ottenuto può essere utilmente confrontato con la frequenza 
 
 

dove  è la parte immaginaria degli autovalori  dello Jacobiano J₁ (in altre parole  è la pulsazione delle oscillazioni (ampliantesi) della corrente x₁ e della tensione x₂ nell'intorno dell'origine). Poichè 
 

si ottiene: