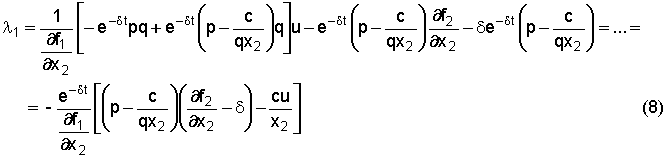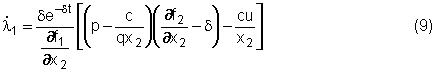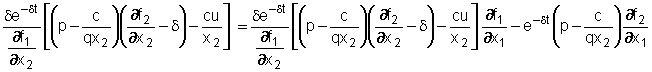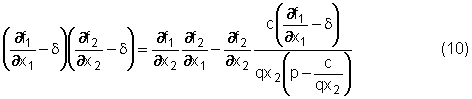Naturalmente
in un modello di questo tipo sarebbe necessario far dipendere i parametri
di crescita, mortalità e fecondità dall’abbondanza di cibo,
che a sua volta dipende dal numero e dal tipo di animali presenti.
Un
modello di questo tipo è tuttavia così complesso da rendere
impossibile una qualsiasi trattazione analitica e conseguente discussione
generale.
Si
può ragionevolmente ipotizzare che in assenza di predatori (x2
= 0) la vegetazione si sviluppi secondo un modello logistico.
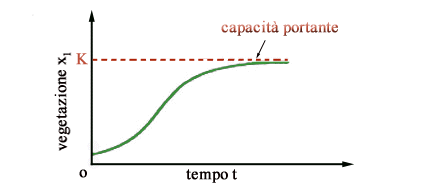
Ciò
significa che in assenza di erbivori e partendo da bassi valori, la vegetazione
cresce secondo una curva sigmoide e tende asintoticamente ad un equilibrio
naturale (stabile), pari alla capacità portante K come mostrato
in figura 1.
D’altra
parte ogni predatore divora una certa quantità di biomassa vegetale
nell’unità di tempo. Questo tasso di predazione pro capite è
in generale crescente con la quantità di risorsa disponibile perchè
quando la vegetazione è più abbondante l’ungulato perde meno
tempo per trovare il cibo. Tuttavia, all’aumentare della risorsa x1,
il tasso di predazione pro-capite tende a saturare a causa della capacità
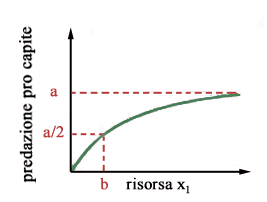
limitata dell’apparato digerente dell’animale. Una funzione che bene interpreta
questo fenomeno è la funzione ax1/(b + x1)
che è mostrata in figura 2.
Il parametro a rappresenta la massima quantità di risorsa di cui l’ungulato è capace di cibarsi nell’unità di tempo, mentre il parametro b rappresenta la densità della risorsa a cui la predazione dell’ungulato è metà del suo valore massimo. In conclusione, l’equazione che descrive la dinamica della preda è la seguente Per
quanto riguarda gli ungulati possiamo supporre che il tasso di accrescimento
pro-capite (natalità e sviluppo) sia proporzionale (secondo un fattore
di efficienza e ) al tasso di predazione pro-capite ax1/(b+x1)
e che il tasso di mortalità m sia invece costante (in realtà
per alte densità x2 tale tasso di mortalità può
aumentare a causa della maggior probabilità di propagazione di epidemie
tra gli animali). La dinamica degli ungulati in condizioni naturali è
pertanto la seguente
Nel caso gli ungulati siano invece sfruttati dall'uomo questa equazione va opportunamente modificata tenendo conto del tasso di cattura. Questo termine può essere assunto proporzionale (secondo un coefficiente di catturabilità q) al prodotto dello sforzo u per il numero x2 di animali presenti sul territorio. Lo sforzo u(t) rappresenta il numero di addetti (cacciatori) che all'istante di tempo t sta cercando di catturare un animale. Poiché il numero di addetti è ovviamente limitato, la variabile u(t) sarà limitata sia inferiormente che superiormente 0 £ u(t) £ umaxSe u(t) = 0 per un certo periodo di tempo, significa che durante tale periodo il sistema non viene sfruttato. Al contrario se u(t) = umax significa che tutti gli addetti alla caccia sono impegnati a tempo pieno nelle operazioni di cattura. In conclusione, l'equazione che descrive gli ungulati è la seguente Gestire
l’allevamento significa fissare una regola che permetta di determinare
lo sforzo u in ogni istante. Tale regola non può essere altro che
una legge di controllo
u(t) = u (x1(t), x2(t)) (3) che
fa dipendere la variabile di controllo u dalle variabili di stato x1
e x2.
La
legge di controllo (3) può essere determinata con vari criteri.
Un primo criterio è quello della semplicità della gestione
che porta alla implementazione della politica a sforzo costante. In altre
parole la (3) diventa
u = u = costante e
questo permette di gestire l’allevamento senza dover effettuare stime dell’abbondanza
della vegetazione (misura di x1(t) ) né conte di animali
(misura di x2(t)).
Un
secondo criterio, decisamente più razionale anche se più
sofisticato, consiste nel determinare la (3) ottimizzando il beneficio
netto dell’azienda. Se l’allevamento non è a termine e quindi l’orizzonte
di gestione è infinito, questo criterio porta a ricercare tra tutte
le politiche di gestione ammissibili quella che massimizza il funzionale
che rappresenta il beneficio netto attualizzato, cioè
dove d
è il tasso di interesse deinflazionato (cioè la differenza
tra il tasso di interesse e il tasso di inflazione), p è il prezzo
deinflazionato di un animale e c è il costo, sempre deinflazionato,
di una unità di sforzo. In questo caso il problema è quindi
formulato come problema di controllo ottimo.
GESTIONE
A SFORZO COSTANTE
Se
lo sforzo è costante ( u = u ) il sistema è descritto
dalle equazioni
e
quindi la dinamica dell’ecosistema è del tutto simile a quella naturale:
l’unica differenza sta nell’aumento della mortalità
da m a (m + q u ).
Gli
equilibri del sistema si trovano annullando le derivate dx1/dt
e dx2/dt. Imponendo
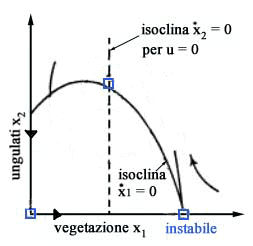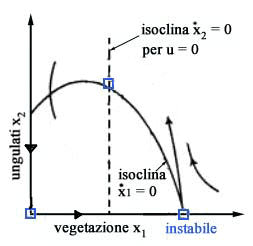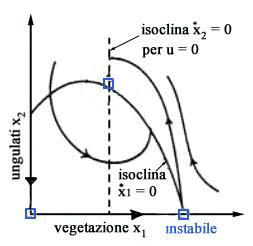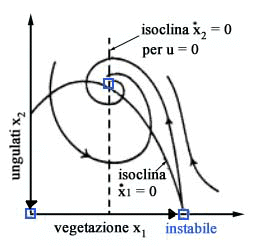
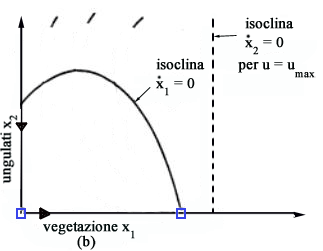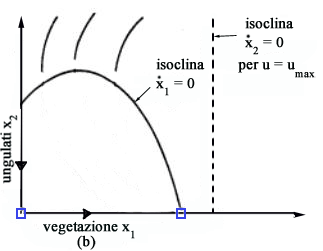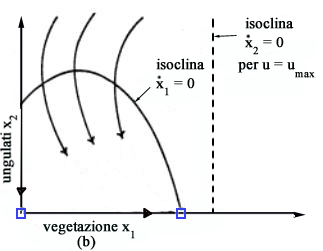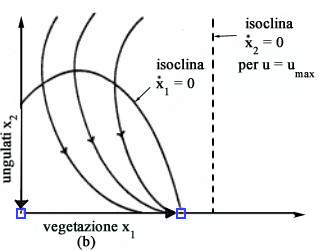
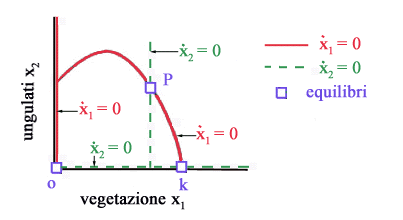
dx1/dt = 0 otteniamo due isocline (vedi Fig.
3)
x1 = 0 ( asse x2 ) x2 = r/a( b + x1 ) ( 1 - x1/K ) ( parabola ) mentre
imponendo dx2/dt =0 otteniamo altre due isocline
x2 = 0 ( asse x1 ) x1 = [( m + q u ) b]/( e a - m - q u) ( retta verticale ) Poiché
l’intersezione di una isoclina dx1/dt = 0 con una isoclina dx2/dt
= 0 fornisce uno stato di equilibrio, si deduce immediatamente che nel
caso in esame gli stati di equilibrio sono tre: l’origine (assenza totale
di vegetazione e ungulati), il punto x1 = K, x2 =
0 (assenza di ungulati e vegetazione alla capacità portante) e il
punto P che rappresenta l’equilibrio di interesse perché è
l’unico in cui è possibile la coesistenza di ungulati e vegetazione.
Al
variare dello sforzo u il punto P si sposta lungo la parabola perchè
l’isoclina x2 (la retta verticale di Fig.
3) si sposta verso destra all’aumentare di u.
Linearizzando
il sistema nell’intorno degli equilibri si può dimostrare che i
primi due sono selle e che il punto P è un fuoco stabile o un nodo
stabile purché sia alla destra del
massimo della parabola dx1/dt = 0 (la dimostrazione è
lasciata al lettore).
Se
in condizioni naturali ungulati e vegetazione sono in equilibrio significa
che per u=0 il punto P è a destra del massimo della parabola
ed è quindi stabile. Questo significa che, almeno in questo caso,
l’implementazione di una politica a sforzo costante non è destabilizzante.
Lo
sforzo u deve tuttavia essere mantenuto inferiore al valore critico
ucrit = 1/q [Kea/(k+b) - m] per
il quale l’isoclina dx2/dt = 0 (la retta verticale di Fig. 3)
passa per il punto x1 = K, x2 = 0, perché
altrimenti non esistono equilibri “produttivi” caratterizzati da valori
di x2 diversi da
zero (in queste condizioni l’equilibrio x1 = K, x2
= 0 è stabile). Poiché il tasso di cattura
è data da q u x2, segue che, all’equilibrio, il tasso
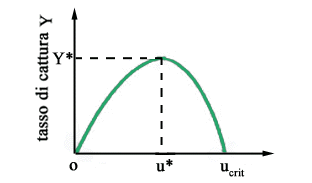
di cattura y è
y = q ux2 = r b e q u/(e a - m - q u) [1-b/K (m + q u)/(e a - m - q u)] Questa
funzione y ( u ) si annulla per u = 0 e per u
= ucrit ed è del tipo mostrato in Fig.
4.
Il
valore y*
del tasso di cattura è noto come “massima produzione sostenibile”
e il corrispondente valore u*
dello sforzo è quello che questa analisi all’equilibrio suggerisce
come valore ottimo per la politica a sforzo costante. Naturalmente, quando
il sistema non è all’equilibrio e lo sforzo viene mantenuto costante
e pari a u*,
si hanno dei transitori, per esempio del tipo di quelli mostrati in
Fig. 5, che tendono asintoticamente verso l’equilibrio di massima
produzione sostenibile (per la verità per fare questa affermazione
bisognerebbe dimostrare che non esistano cicli limite).
Ogni
deviazione dall’equilibrio ottimo P*,
come quella dovuta ad una moria di ungulati conseguente ad una epidemia
(punto A di Fig. 6), o ad un incendio
(punto B) o all’immissione di ungulati dall’esterno (punto C) o a un inverno
molto mite che faciliti lo sviluppo della vegetazione (punto D), dà
luogo a transitori durante i quali la gestione a sforzo costante non è
in generale ottima dal punto di vista della produzione di biomassa.
Poiché perturbazioni di questo o altro tipo sono la norma anziché l’eccezione, si comprende come la gestione a sforzo costante possa essere messa giustamente in discussione. In particolare, quello che non sembra corretto in tale tipo di gestione è il fatto che, dopo una perturbazione che allontana il sistema dall’equilibrio a massima produzione sostenibile, lo sforzo non venga modulato in modo da riportare rapidamente il sistema verso tale equilibrio. GESTIONE OTTIMALE Per risolvere il problema di controllo ottimo (1, 2, 4) possiamo usare il principio del massimo. Per questo definiamo la funzione hamiltoniana H = e-dt (p q u x2 - c u) + l1 f1(x1, x2) + l2 f2(x1, x2) - l2 q u x2 == [ e-dt (p q x2 - c) - l2 q x2 ] u + [ l1 f1(x1, x2) + l2 f2(x1, x2) ] La
funzione hamiltoniana è lineare nella variabile di controllo u e
quindi la sua massimizzazione fornisce la seguente regola
dove
s(t) = e-dt (p q x2 - c) - l2 q x2 Esaminiamo
allora la condizione di singolarità s(t)
= 0 (per un intero intervallo di tempo) e dimostriamo che esiste un arco
singolare caratterizzato da valori costanti di x1, x2
e u (cioè dimostriamo che esiste un equilibrio singolare). La condizione s(t)
= 0 fornisce
l2 = e-dt(p q x2 - c)/(q x2) = e-dt(p - c/q x2)(5) da
cui, derivando rispetto a t e ipotizzando che x2 sia costante,
segue che
Dal
principio del massimo segue peraltro che
La
seconda di queste due relazioni (che definiscono la dinamica delle variabili
“aggiunte” l1
e l2)
risolta rispetto al1 fornisce
:
che,
tenendo conto della (5) e (6), diventa
Derivando
rispetto a t questa relazione, sempre tenendo conto che x1,
x2 e u sono costanti, segue che
che
può essere sostituita insieme alla (2) con dx2/dt=0,
alla (8) ed alla (5) nella (7) dando così:
Dividendo
per e-dt,
moltiplicando per ¶f1/¶x2
e
raccogliendo opportunamente alcuni termini, si ottiene infine:
che
è una condizione nelle sole variabili x1 e x2.
La
(10) insieme alle due relazioni:
dà
luogo ad un sistema di tre equazioni in tre incognite la cui soluzione
individua l’arco singolare. In realtà, per determinare l’equilibrio
singolare è sufficiente considerare la (10) e l’equazione f1
= 0 che costituiscono un sistema di due equazioni nelle due incognite x1
e x2. Risolto questo sistema, si può utilizzare la relazione
f2 - q u x2 = 0 per ricavare immediatamente il valore
using della variabile di controllo.
Nel
caso in cui il costo unitario c dello sforzo sia trascurabile (come spesso
è negli allevamenti di ungulati) la condizione di singolarità
(10) diventa:
e
si semplifica ulteriormente se il tasso di interesse è nullo, diventando
Come
già detto, tutte queste condizioni di singolarità vanno abbinate
alla relazione f1 = 0 che impone l’equilibrio. Se pertanto si
suppone che all’equilibrio x1¹0,
quest’ultima condizione afferma che (vedi equazione (1)):
x2
= r/a ( b + x1 ) ( 1 - x1/K
)
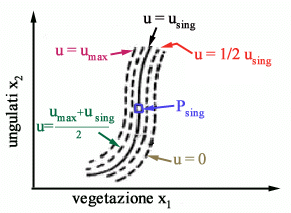
che
è l’equazione dell’isoclina a forma di parabola già esaminata
nel caso di gestione a sforzo costante. In altre parole l’equilibrio singolare
è un punto Psing che sta sulla parabola di Fig.
3 (vedi anche Fig. 8). Per d=0
tale punto coincide con il punto di equilibrio P*a
massima produzione sostenibile, mentre per d >0
il punto Psing è spostato verso destra rispetto a P*
(questa proprietà si ricava facilmente applicando il teorema del
Dini alla (11) e dimostrando che ¶x2/¶d
< 0). Ciò significa che più alto è il tasso di
interesse più intenso è, a regime, lo sfruttamento dell’allevamento,
così che per valori molto elevati del tasso di interesse si può
arrivare alla situazione limite in cui la politica ottima è quella
di abbattere tutti gli ungulati.
Per
poter concludere si dovrebbe ora dimostrare che non esistono altri archi
singolari al di fuori di quello già trovato (equilibrio). Questa
dimostrazione non è certamente banale come la precedente e questo
è probabilmente il motivo per cui non è stata ancora fatta.
Esistono tuttavia buoni motivi, come l’analogia con il caso più
semplice di sfruttamento di una singola risorsa e i risultati ottenuti
numericamente con la programmazione dinamica su casi specifici, che portano
a congetturare che non esistano altri archi singolari. In questa ipotesi,
la regola di gestione ottimale è quindi caratterizzata da tre soli
possibili valori dello sforzo: u=0, u=using, u=umax
e lo sforzo using va esercitato soltanto quando il sistema si
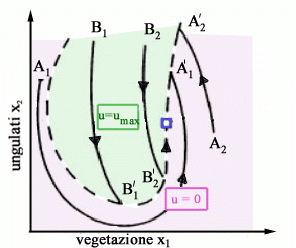
trovi nell’equilibrio singolare. Nello spazio di stato (x1,
x2) le traiettorie ottime per u=0 sono come in Fig.
7a mentre quelle per u=umax sono come in Fig.
7b.
Due
traiettorie tra quelle mostrate in Fig. 7a e
7b
sono
particolarmente importanti: quelle che per u=0 e per u=umax
passano
per il punto Psing sulla parabola dx1/dt
= 0.
Queste
due traiettorie dividono il primo quadrante in due sottoregioni
come mostrato in Fig. 8.
Se la condizione iniziale è il punto A, allora lo sforzo è nullo e il sistema evolve fino a raggiungere il punto Psing dove si commuta istantaneamente a u=using. Se invece la condizione iniziale è il punto B di Fig. 8, allora lo sforzo è massimo finché si raggiunge Psing dove si commuta a u=using. In Fig. 9 sono mostrate le traiettorie ottime corrispondenti a qualsiasi condizione iniziale. Se si
parte da A1 o A2 non si catturano animali finché
la traiettoria interseca la separatrice della regione u=0 dalla regione
u=umax (punti A'1 e A'2).
A quel punto si commuta da u=0 a u=umax e si scende così
lungo la separatrice fino all’equilibrio singolare Psing , raggiungendo
il quale si commuta di nuovo da u=umax a u=using.
Similmente se si parte da B1 o B2 si sfrutta il sistema a massimo sforzo fino al punto B'1 o B'2 e poi ci si astiene completamente dal catturare animali finché si raggiunge l’equilibrio singolare. La politica di gestione ottimale si distingue quindi da quella a sforzo costante (anche nel caso c=0 e d=0) e la differenza riguarda proprio il modo con cui l’equilibrio ottimo viene riavvicinato dopo una perturbazione. Se, ad esempio, si considera il periodo iniziale di gestione di un allevamento ottenuto popolando un territorio con vegetazione alla capacità portante con un certo numero di ungulati, si ottengono le due traiettorie mostrate in Fig. 10a e 10b. La prima
mostra un lento avvicinamento all’equilibrio, mentre la seconda è
costituita da un primo tratto di traiettoria (u=0) durante il quale gli
ungulati si sviluppano al massimo a causa della grande abbondanza di vegetazione
seguito da un secondo tratto durante il quale gli animali vengono catturati
il più rapidamente possibile.
Questo secondo tratto di traiettoria è quindi molto rapido e quasi verticale nello spazio di stato: in pratica le operazioni di cattura sono così concentrate che la vegetazione non ha il tempo di variare. Tutta questa analisi mostra che per gestire in modo ottimale un allevamento di ungulati è essenziale stimare sia la vegetazione x1 che il numero di animali x2, perché solo così si riesce a sapere se ci si trova nella regione in cui è corretto applicare il massimo sforzo o in quella in cui è bene astenersi dal catturare animali. Per di più, dato che nell’intorno dell’equilibrio Psing la frontiera che separa le due regioni è verticale, risulta particolarmente importante stimare con precisione la biomassa vegetale, un fatto che è stato solo recentemente segnalato in letteratura. Nella realtà, un allevamento è sempre soggetto a tutta una serie di più o meno forti “disturbi” del tutto imprevedibili. L’applicazione rigorosa della politica di controllo ottimale darebbe quindi luogo a frequentissime commutazioni nello sforzo, perché sarebbe ovviamente frequente che lo stato del sistema si sposti da una parte all’altra della frontiera che separa la regione con u=0 da quella con u=umax. Per evitare questo inconveniente si può pensare di adattare artificiosamente la politica di controllo u(x1,x2), ad esempio, come mostrato in Fig. 11.
In effetti
politiche di gestione proprio di questo tipo sono state recentemente ricavate
risolvendo numericamente (con la programmazione dinamica) un problema di
controllo stocastico simile a quello qui considerato. A conclusione di
questa analisi è bene richiamare l’attenzione su almeno due punti
importanti. In primo luogo va notato che le proprietà della gestione
ottimale qui messe in evidenza sono solo da intendersi come alcune delle
proprietà importanti nella gestione effettiva di un allevamento.
Altre proprietà, come quelle sulla scelta degli animali da abbattere,
possono essere ricavate formalmente solo con modelli più complicati
che differenzino animali di diverso sesso ed età. In secondo luogo
è doveroso osservare che anche nel caso di allevamenti molto omogenei
e facilmente studiabili è difficile poter conoscere con precisione
il valore numerico di tutti i parametri del modello (capacità portante
K e coefficiente di crescita r della vegetazione, mortalità m, efficienza
e predazione pro capite (a e b) degli ungulati, nonché i coefficienti
tecnici (q) ed economici (d, p
e c) del problema). L’analisi qui fatta con il principio del massimo è
quindi da ritenersi di tipo più qualitativo che quantitativo, nel
senso che essa fornisce solo generici suggerimenti sul comportamento da
seguire più che precise regole operative da implementare.
|

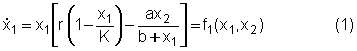

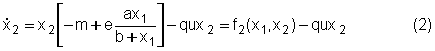
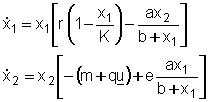


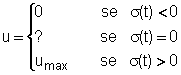

 (7)
(7)