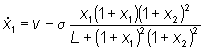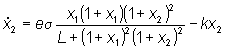| Poichè la dinamica delle concentrazioni di
substrato e cellule è descritta da un sistema autonomo del secondo
ordine, si tratta di verificare che il sistema ha un attrattore e che tale
attrattore è un equilibrio per bassi e alti valori del flusso di
nutriente v e un ciclo per valori intermedi di v.
Dalla descrizione degli esperimenti sembra che il ciclo appaia e scompaia al variare di v secondo una biforcazione di Hopf. Questo fatto può essere appurato studiando gli autovalori dello Jacobiano o simulando il sistema per diversi valori del parametro. IL MODELLO: Dalle informazioni disponibili segue che la dinamica
della reazione biochimica è descritta dal seguente sistema autonomo
del secondo ordine:
INTERPRETAZIONE
DEGLI ESPERIMENTI:
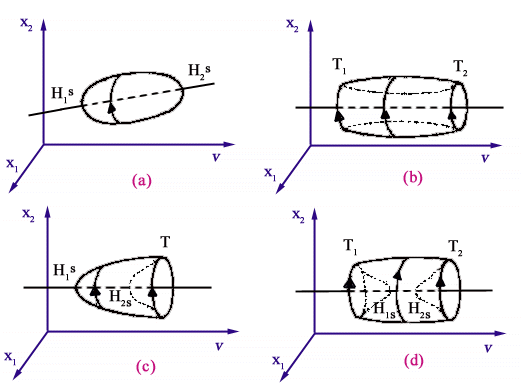
Si può notare che nel caso (a) si ha
un unico attrattore (equilibrio o ciclo) per tutti i valori di v,
mentre negli altri tre casi per certi valori del parametro v si
hanno due attrattori. Si può pertanto propendere a favore della
prima ipotesi, perchè l'esistenza di attrattori multipli avrebbe
reso i risultati degli esperimenti dipendenti dalle condizioni iniziali,
un fatto che sarebbe certamente stato notato o che avrebbe reso impossibile
l'interpretazione dei risultati. Il problema consiste quindi nel verificare
che il modello (1,2) ha, al variare di v, due biforcazioni di Hopf
supercritiche.
EQUILIBRI E BIFORCAZIONI
DI HOPF:
che può essere scritta nella forma:
con
ma dato che vL>>A si può
concludere che esiste un unico stato di equilibrio L'unicità dello stato di equilibrio (positivo)
esclude la possibilità di biforcazioni omocline che necessiterebbero
l'esistenza di due stati di equilibrio. Ciò conferma quanto ipotizzato
nel paragrafo precedente.La stabilità dell'equilibrio si può
studiare calcolando gli autovalori dello Jacobiano e la presenza di eventuali
biforcazioni di Hopf è rivelata dall'annullamento della parte reale
di una coppia di autovalori complessi coniugati dello Jacobiano. In pratica,
questi calcoli non sono eseguibili analiticamente in questo caso, per cui
è necessario ricorrere ad un package che esegua automaticamente
la linearizzazione e calcoli gli autovalori dello Jacobiano. Così
facendo si può constatare facilmente che gli autovalori dello Jacobiano
sono complessi e che la loro parte reale è negativa per bassi e
per alti valori di v e positiva per valori intermedi. Ciò
permette di eliminare il caso (b) di Fig.1
come caso possibile. Per individuare in quale dei tre rimanenti casi ci
si trova si dovrebbe calcolare il cosiddetto "numero di Liapunov" della
biforcazione di Hopf, il cui segno permette di dire se la biforcazione
è subcritica o supercritica. Per sciogliere l'enigma si può
pensare, molto più semplicemente, di eseguire alcune simulazioni,
per valori crescenti del parametro v, a partire dallo stato iniziale
che è comunque vicino all'equilibrio.
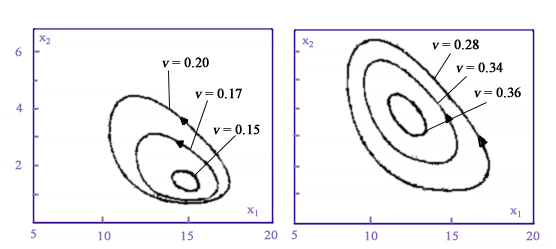
SIMULAZIONI:
I punti riportati sui cicli di Fig.2 marcano istanti di tempo tra loro intervallati di 10[s]. Si può così constatare che il modello spiega anche la diminuzione del periodo con il flusso di alimentazione, proprietà notata dagli sperimentatori.
|