soluzione piene Ticino

in cui V(t) è il volume d’acqua invasato nel lago all’istante t, p(t) è la precipitazione sullo specchio d’acqua nell’unità di tempo, w(t) è la somma di tutte le rimanenti portate di afflusso (immissari, ruscellamento, infiltrazione e scarichi), e(t) è la portata di evaporazione e r(t) è la portata dell’emissario (rilascio).

Se si suppone che lo specchio d’acqua sia un piano sempre parallelo a se stesso, il volume V(t) è in realtà funzione del livello x(t) in un punto qualsiasi del lago, per esempio all’imbocco dell’emissario (Sesto Calende). Nel caso del lago Maggiore la superficie S del lago non varia sensibilmente con il livello x(t) del lago per cui

così che la (1) può essere riscritta come

Questa equazione differenziale, discretizzata con il metodo di Eulero con un intervallo di tempo pari all’ora, diventa:

in cui t è un numero intero che indica l’ora, x(t) è il livello del lago a Sesto Calende all’inizio dell’ora t e p(t), w(t), e(t), r(t) sono volumi di afflusso e deflusso durante l’ora t.

Se il livello x è il livello del lago all’imbocco dell’emissario e se in tale punto non si hanno rilevanti fenomeni di rigurgito, il rilascio r è in ogni istante univocamente legato al livello x dalla scala di deflusso,

Poiché le variazioni di livello in un periodo di tempo breve come l’ora sono comunque molto contenute, possiamo ipotizzare che il volume (m³) di deflusso r(t) durante l’ora t non si discosti sensibilmente rispetto alla portata (m³/h) all’inizio dell’ora e scrivere nella (2)

Le equazioni (2) e (3) possono essere usate per effettuare le previsioni r*(t+k/t) (secondo il seguente schema recursivo):

all’inizio di ogni ora t, quando sono ormai noti x(t) e tutti i volumi di afflusso nelle ore precedenti (t-1), (t-2),….

Ad ogni passo dello schema si calcolano x*(t+k/t) e r*(t+k/t), eccezion fatta per il primo passo in cui x*(t/t) non deve essere calcolato dato che esiste già il rilievo diretto x(t). Perché lo schema possa essere reso operativo si devono precisare le regole di calcolo delle previsioni di pioggia p*(t+k/t), di evaporazione e*(t+k/t) e di afflusso w*(t+k/t).

E’ noto che l’intensità della pioggia è molto variabile sia nello spazio che nel tempo, per cui la previsione del volume d’acqua che precipita in un’ora su una regione è un operazione decisamente ardua. Esperimenti effettuati su numerosi casi hanno mostrato che l’ipotesi di congelamento

fornisce risultati quasi altrettanto attendibili di quelli che si ottengono con previsori più sofisticati, a meno che siano disponibili informazioni spazio-temporali dettagliate come quelle rilevate da un radar meteorologico. Poiché nel caso in esame si hanno solo quattro telepluviometri è ragionevole fare per ognuna delle quattro stazioni l’ipotesi di congelamento e stimare l’afflusso meteorico totale sullo specchio lacuale come combinazione convessa delle misure

in cui i coefficienti di influenza y_idevono soddisfare le relazioni

Per valutare i coefficienti di influenza è stato usato il metodo dei poligoni, la cui applicazione è illustrata in figura.

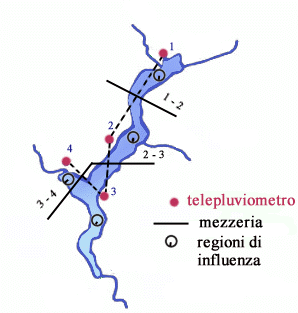
Per prima cosa si tracciano le mezzerie dei segmenti che congiungono a due a due le stazioni di misura (in figura sono riportate solo la 1-2, la 2-3 e la 3-4 perché sono le uniche che contano) e si individuano così le regioni di influenza di ogni singolo pluviometro. Dette S₁, S₂, S₃ e S₄ le superfici lacuali di tali regioni, i coefficienti di influenza sono dati da

Questo metodo di stima della precipitazione totale a partire dai quattro dati puntuali e l’ipotesi di congelamento sono decisamente rozzi. D’altra parte il termine p(t) nella (2) è piccolo, se non proprio trascurabile, rispetto a w(t) e a r(t) per cui non sembra ragionevole sofisticare ulteriormente il metodo.

L’evaporazione dipende dalle condizioni meteorologiche locali, per cui la sua previsione non può essere effettuata con i soli dati a disposizione. D’altra parte, anche se fossero disponibili dati meteorologici per poter stimare all’inizio dell’ora t l’evaporazione nelle ore successive sarebbe necessario effettuare innanzitutto delle previsioni meteorologiche, in particolare di velocità del vento, operazione quanto mai difficoltosa.

In conclusione, non si può far altro che fissare e*(t+k/t) uguale al valor medio dell’evaporazione nella stagione considerata. Dato poi che nei periodi di piena il termine e(t), nella (2) è comunque del tutto trascurabile rispetto a r(t), nelle elaborazioni numeriche si è posto:

PREVISIONE DELL'AFFLUSSO

I quattro immissari principali (Toce, Tresa, Maggia e Ticino) sono responsabili di una buona parte dell’afflusso totale al lago. Per stimare bene l’afflusso totale è tuttavia opportuno maggiorare la portata di afflusso a_i in modo da tener conto del ruscellamento e sostituire pertanto la portata di afflusso a_i con la portata maggiorata u_i = a_ia_i con a_i > 1. Fatta questa operazione si può scrivere:

Per calcolare le previsioni w*(t+k/t) si può decidere di estrapolare polinomialmente i dati. All’inizio dell’ora t, quando sono noti u_i(t-1), u_i(t-2), ... ,si può effettuare un’estrapolazione, ad esempio, parabolica, e valutare così, sulla base degli ultimi tre dati u_i(t-1), u_i(t-2) e u_i(t-3), tutte le portate di afflusso u*_i(t+k/t), per cui risulta

In ultima analisi, le previsioni di afflusso sono basate sui tre ultimi dati di afflusso rilevati con teleidrometri.

Ovviamente, le previsioni di afflusso potrebbero essere affinate, per esempio facendo uso di modelli di previsione tipo ARMAX, qualora fossero disponibili in tempo reale misure sulle precipitazioni nei bacini imbriferi dei quattro immissari principali.

lì modello di previsione messo a punto non necessita di taratura perché tutti i parametri (S, y_i ,a_i) sono già fissati. I dati della piena del 1957 possono pertanto essere direttamente usati per valutare la bontà dello schema di previsione. Si può così calcolare lo scarto quadratico medio tra rilasci previsti r*(t+k/t)e rilasci reali r(t+k) e la correlazione tra questi stessi dati. Lo scarto quadratico medio risulta molto elevato soprattutto per previsioni di qualche ora in avanti: per esempio, lo scarto quadratico medio tra previsioni e realtà è di 300 m³/sec per previsioni di sei ore in avanti, un valore inaccettabile se si pensa che durante il periodo considerato i rilasci sono compresi tra 500 e 1400 m³/sec. Anche la correlazione ha valori troppo bassi per essere accettabile, ad esempio 0,62 per le previsioni di sei ore in avanti.

La conclusione di quest’analisi è che il modello di previsione non è affidabile. Esso va quindi modificato in modo da ottenere un nuovo modello che dia luogo a previsioni accettabili. Naturalmente la modifica va apportata dopo aver individuato, se possibile, i motivi di debolezza del modello. Nel caso specifico ciò non è difficile, dato che, tra tutte le ipotesi fatte per semplificare il modello, una è decisamente sospetta: quella che la superficie del lago sia un piano di inclinazione fissa. Questa ipotesi implica infatti che una variazione della portata di uno degli immissari si faccia istantaneamente sentire sull’emissario (vedi equazioni (2) e (3). E’ scontato invece che sia necessario un certo tempo perché la portata dell’emissario risenta di una variazione di portata di uno degli immissari. Per migliorare le previsioni è quindi possibile che basti tener conto almeno approssimativamente del fenomeno della propagazione dell’onda di piena.

Per descrivere il fenomeno della propagazione, in teoria si dovrebbe far uso di equazioni differenziali alle derivate parziali del tipo di quelle di De Saint Venant. Si può tuttavia immaginare che il fenomeno possa essere in prima approssimazione descritto dalla (2) in cui si introducano dei ritardi di tempo fissi t₁, t₂, t₃e t₄ sulle portate degli immissari. Così facendo una variazione della portata del primo immissario si concretizza in una variazione di livello a Sesto Calende soltanto t₁ ore dopo e quindi, a causa della (3), il rilascio risente con t₁ore di ritardo della variazione di portata dell’immissario. In conclusione, il nuovo modello è formalmente ancora rappresentato dalle equazioni (2) e, (3) in cui tuttavia l’afflusso w(t) è l’afflusso ritardato.

Lo schema di calcolo delle previsioni r*(t+k/t) è pertanto ancora quello precedente. L’unica differenza sta nel fatto che per effettuare le previsioni w*(t+k/t) si usa questa volta l’equazione

w*(t+k/t) = S_i u*_i(t - t_i+k/t) (7)

anziché la (5). Pertanto i termini u*(t-t_i+k/t) sono in realtà dei dati e non delle previsioni se k<t_i.

Il modello con ritardi fissi ha quattro parametri da tarare: i ritardi t₁, t₂, t₃ e t₄. Questi parametri devono essere numeri interi per cui non esistono per la loro determinazione formule chiuse come quella della stima ai minimi quadrati. Per determinare i valori ottimali t°_ida assegnare ai ritardi t_iè pertanto necessario far uso dei dati della piena del 1957 e provare (in linea di principio) tutte le combinazioni della quaterna di numeri interi (t₁,t₂,t₃,t₄) e scegliere come ottimale quella che fornisce globalmente le migliori previsioni. Naturalmente si deve precisare il criterio con cui giudicare la bontà delle previsioni.

Usando come criterio la minimizzazione dell’errore quadratico delle previsioni di rilascio nell’ora t, cioè

dove la sommatoria è estesa a tutti i giorni t della piena del 1957, si trova che la combinazione migliore dei ritardi è la seguente

Le prestazioni del previsore sono questa volta accettabili. Le correlazioni tra previsioni e realtà sono pari a 0.99 per k = 0, 1,…., 6 e si abbassano soltanto a 0.98 e 0.97 per k = 7 e k = 8 (si noti che a causa della (7) solo questi ultimi valori di k implicano l’uso di vere previsioni di afflusso u_i). L’errore quadratico medio è pure molto contenuto: 5 m³/sec per k = 1, 16 m³/sec per k = 3, 32 m³/sec per k = 6 e 60 m³/sec per k = 8. Quest’ultimo valore è particolarmente significativo e dice che anche le previsioni più difficili, quelle su un intervallo di otto ore, sono accettabili perché hanno un errore quadratico medio di 60 m³/sec a confronto di valori reali di rilascio compresi tra 500 e 1400 m³/sec. Ciò significa che gli errori sono mediamente inferiori al 10% e sono quindi paragonabili agli errori di misura. Esiste infine un’ultima considerazione, che in un certo senso è la più confortante di tutte: i ritardi t⁰_i sono con ottima approssimazione proporzionali alle distanze tra Sesto Calende e il punto di misura (teleidrometro) e ciò significa che i ritardi di tempo introdotti nel modello interpretano veramente il ritardo della propagazione dell’onda di piena nel lago. Per verificare ulteriormente la validità di questo modello di previsione si può sviluppare un nuovo modello, più generale di quello a ritardi fissi, per constatare se ciò fornisce vantaggi significativi. In caso contrario ci si accontenterà del modello a ritardi fissi.

L’equazione (6) e la corrispondente equazione (7) possono essere rilassate nel modo seguente

ciò significa che l’afflusso w(t) nell’equazione (2) è calcolato come “media mobile” degli afflussi dei quattro immissari principali. Il modello a ritardi fissi è ovviamente un caso particolare di quello a media mobile (Q_ij = 1 per j=t_i e Q_ij = 0 per j ¹t_i).

I parametri del modello sono i quattro numeri interi n₁, n₂, n₃, e n₄ e i coefficienti Q_ij della media mobile. I primi si possono fissare a priori, maggiorando ragionevolmente i ritardi fissi t⁰₁, t⁰₂, t⁰₃ e t⁰₄, ad esempio, nel modo seguente

I rimanenti parametri Q_ij sono n₁+n₂+n₃+n₄ = 59. Per stimarli si può procedere in modo euristico, calcolando all’inizio di ogni ora (t+1) l’afflusso w(t) per mezzo della (2) e applicando il criterio dei minimi quadrati alla (8) in cui w(t) e u_i(t-j) sono noti. Per questo si può applicare la formula classica dei minimi quadrati

dove Q_t é il vettore della stima dei parametri (Q₁₁, Q₁₂, ..., Q₂₁, Q₂₂, .., Q₄n₄) e la matrice M_t e il vettore y_t dipendono dai dati. Le dimensioni della matrice (M_t^T M_t) che deve essere invertita sono notevoli (59 x 59), per cui é opportuno applicare il metodo della stima recursiva che permette di determinare la stima ottimale dei parametri Qij con i dati dell’intervallo (0,t) senza invertire la matrice (M_t^T M_t). Con questo schema la stima Q_t è calcolata correggendo opportunamente la stima Q_t-1 fatta all’inizio dell’ora precedente: si ha così la possibilità di seguire la taratura del modello e di interpretare i risultati. Ad esempio, nel caso specifico si è visto che la stima dei parametri Q_ij relativi al secondo immissario (il Tresa) risulta molto diversa di ora in ora, mentre le altre stime sono relativamente stabili. Una semplice indagine ha permesso di verificare che i dati rilevati dal telepluviometro posto sul Tresa non sono molto significativi perché tra il punto di misura e il lago Maggiore esiste un piccolo serbatoio per la produzione di energia elettrica. Non è detto pertanto che i deflussi da questo serbatoio siano strettamente legati ai dati rilevati a monte e questo spiega l’anomalia nella stima dei parametri Q_ij.

Le previsioni effettuate in questo modo sono decisamente affidabili. La correlazione tra previsioni e realtà è 0.99 anche per periodi di otto ore. L’errore quadratico medio è leggermente inferiore che nel caso del modello a ritardi fissi per periodi di previsione inferiore a sei ore. Per previsioni di sette e otto ore in avanti le prestazioni sono invece leggermente inferiori a quelle del modello con ritardi fissi.

In conclusione, quindi, non sembra che le previsioni del modello a media mobile siano apprezzabilmente migliori di quelle che si ottengono col modello a ritardi fissi. D’altra parte quest’ultimo modello non necessita di elaborazioni numeriche in tempo reale, come invece lo schema a media mobile richiede. Sembra pertanto preferibile realizzare le previsioni per mezzo del modello a ritardi fissi.