MOLTEPLICITA' DI SOLUZIONI PERIODICHE:

Un sistema non lineare forzato periodicamente è un sistema descritto da equazioni di stato del tipo
 
 

(1)

con:
 

(2)

Tipicamente, in un sistema non lineare esiste una soluzione periodica stabile, detta fondamentale, dello stesso periodo (T=2p / w) della forzante. Spesso tale soluzione periodica è presente per tutti i valori del parametro p, dell'ampiezza U e del periodo T della forzante e in regioni opportune dello spazio dei parametri (p,U,w) essa è anche globalmente stabile. 
Può tuttavia accadere che in altre regioni dello spazio dei parametri esistano anche soluzioni periodiche di periodo multiplo di quello della forzante. Tali soluzioni, dette subarmoniche, nascono, per esempio, per biforcazione tangente o per raddoppio di periodo quando si fissano p e w nelle (1),(2) e si varia U.

Può così accadere che per valori opportuni dell'ampiezza della forzante il sistema ammetta un unico comportamento periodico stabile (la fondamentale), e che per valori più elevati di U il sistema ammetta invece anche una soluzione subarmonica stabile. 
Se questo è il caso, da un punto di vista pratico il sistema si porterà a funzionare asintoticamente sulla fondamentale o sulla subarmonica a seconda delle condizioni iniziali (e potrà eventualmente commutare da un modo di funzionamento all'altro nel caso agiscano sul sistema dei disturbi consistenti). 
Qualora il sistema funzioni su una subarmonica e l'ampiezza U della forzante venga fatta variare lentamente, il sistema resterà "agganciato" al funzionamento subarmonico finchè questo rimarrà stabile. Ma se, al variare di U, la subarmonica sparisce per biforcazione tangente, il sistema cambierà modo di funzionare (transizione catastrofica da subarmonica a fondamentale). Da un punto di vista sperimentale si noterà quindi un brusco "salto di frequenza".

UN SEMPLICE PROTOTIPO:
Benchè il polmone sia un sistema meccanico complesso, si può pensare che sia lecito, almeno in primissima approssimazione, modellizzarlo come un semplice sistema meccanico (vedi Fig.1) costituito da una massa, da uno smorzatore e da una molla. La forza esercitata dalla molla è molto bassa per piccole elongazioni ma cresce molto più che linearmente con l'elongazione a causa della presenza di consistenti elementi elastici della cassa toracica.
 
 

Fig. 1: Prototipo di sistema meccanico non lineare con forza di richiamo di tipo cubico

Per questo motivo è plausibile che l'essenza di queste non linearità sia catturabile supponendo che la molla eserciti una forza di tipo cubico (vedi Fig.1). 
Fatta questa ipotesi, il polmone è allora descritto dalle seguenti equazioni:
 
 

	(3)
	(4)

in cui a, b, U e w sono parametri costanti caratterizzanti il polmone e la macchina (polmone artificiale).

Per quanto detto in precedenza, si tratta quindi di verificare che il sistema (3,4) ammetta, per valori particolari dei parametri, delle subarmoniche di periodo 3T e che tali subarmoniche nascano per biforcazione tangente. 

SIMULAZIONE:
La verifica dell'esistenza delle subarmoniche e delle relative biforcazioni tangenti può essere fatta per simulazione. 
Fissando, ad esempio, i seguenti valori per i parametri:
 

a=1

b=0.1

w=1

partendo da stato iniziale nullo si ottiene, per U=U₁=0.05, il comportamento periodico (fondamentale) mostrato in Fig.2. Tale comportamento periodico è l'unico possibile (come è facile constatare simulando il comportamento del sistema per numerose condizioni iniziali).
 
 

Fig. 2: Comportamento periodico fondamentale del prototipo

Per valori più elevati di U, per esempio U=U₂=0.15, si individua invece anche un comportamento subarmonico di periodo 3T (per esempio, simulando il sistema a partire dalle condizioni iniziali x₁(0)=-0.41, x₂(0)=0.13).

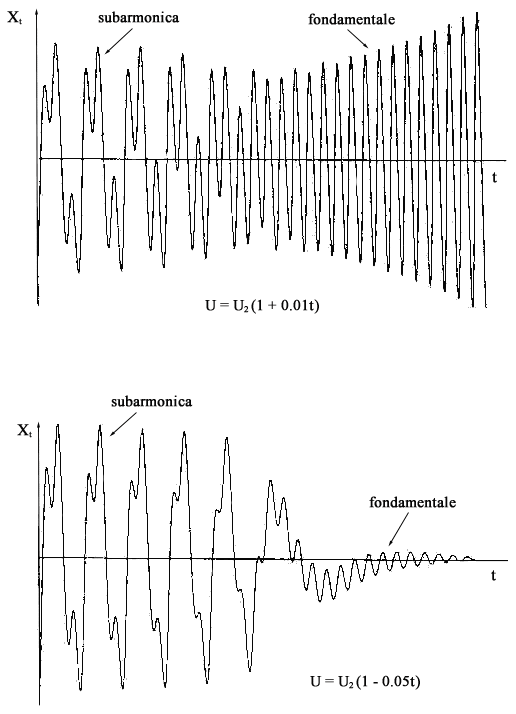
Infine, per evidenziare in modo semplice il fenomeno del salto di frequenza, si può simulare il sistema (3,4) con U lentamente variabile (vedi Fig.3).
 

Fig. 3: Simulazione di un salto di frequenza nel prototipo di Fig.1

Se, ad esempio, si fissa x₁(0)=-0.41, x₂(0)=0.13 e 
 

con e piccolo, la simulazione mostra che il sistema tende rapidamente alla soluzione subarmonica di periodo 3T e salta poi, quando tale soluzione sparisce per biforcazione tangente, sulla soluzione fondamentale. 
Nel caso specifico ciò accade sia incrementando che decrementando U.