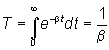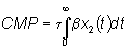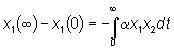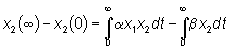| Per risolvere il problema si deve innanzitutto proporre
un modello di epidemia e poi "tarare" i parametri di questo modello usando
i dati disponibili. Indi si deve formalizzare il processo decisionale come
problema di ottimizzazione (minimizzazione del costo sociale rispetto al
numero di vaccinati) e determinare come sia possibile eseguire questa minimizzazione
usando il modello di epidemia.
IL MODELLO:
Indicati con x1(t)
e x2(t) il numero di suscettibili
e infetti all'istante t e supponendo che il numero di persone che
diventano infette tra l'istante t e l'istante (t+Dt)
sia proporzionale, secondo un coefficiente a,
al prodotto x1(t)x2(t)
e al tempo Dt,
si
può scrivere:
| x1(t+Dt)=x1(t)-ax1(t)x2(t)Dt |
(1)
|
Analogamente, supponendo che il numero
di infetti che diventano immuni tra l'istante t e l'istante (t+Dt)sia
proporzionale, secondo un coefficienteb,
al numero di infetti x2(t)
e al tempo Dt,
si
può scrivere:
| x2(t+Dt)=x2(t)+ax1(t)x2(t)Dt-bx2(t)Dt |
(2)
|
Per Dt
-->0 le (1,2) diventano:
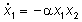 |
(3)
|
 |
(4)
|
che sono le equazioni di stato di un sistema
non lineare del secondo ordine.
Il sistema (3,4) è un sistema autonomo
positivo perchè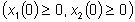 implica implica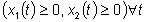 . .
Il comportamento del sistema va quindi
studiato soltanto nel primo quadrante dello spazio di stato (x1,x2).
Il sistema ha come stati di equilibrio tutti i punti
dell'asse x1 (popolazione costituita
esclusivamente da suscettibili).
L'isoclina 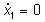 è data dagli assi coordinati, mentre l'isoclina
è data dagli assi coordinati, mentre l'isoclina 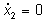 è data dall'asse x1 e dalla
retta verticale di equazione x1=b/a.
è data dall'asse x1 e dalla
retta verticale di equazione x1=b/a.
Lo Jacobiano del sistema valutato nell'equilibrio 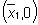 è:
è:
Gli autovalori dello Jacobiano sono l1=0
e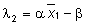 . .
Pertanto, per 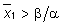 (cioè a destra dell'isoclina
(cioè a destra dell'isoclina 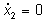 )
il sistema linearizzato ha un autovalore positivo (instabilità forte)
e quindi l'equilibrio ( )
il sistema linearizzato ha un autovalore positivo (instabilità forte)
e quindi l'equilibrio ( )
è instabile. )
è instabile.
Per 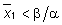 il sistema linearizzato è invece semplicemente stabile per cui il
metodo della linearizzazione non permette di trarre conclusioni sulla stabilità
dell'equilibrio (
il sistema linearizzato è invece semplicemente stabile per cui il
metodo della linearizzazione non permette di trarre conclusioni sulla stabilità
dell'equilibrio ( ).
In realtà, l'analisi del segno di ).
In realtà, l'analisi del segno di  e
e 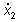 nell'intorno di (
nell'intorno di ( )
permette immediatamente di concludere che ( )
permette immediatamente di concludere che ( )
è semplicemente stabile come mostrato in Fig.1. )
è semplicemente stabile come mostrato in Fig.1.
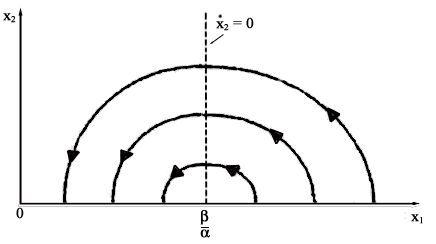 |
| Fig.
1: Quadro delle traiettorie del
sistema (3,4) |
Le traiettorie di Fig.1
evidenziano che l'epidemia si innesca soltanto se x1(0)>b/a
e che il numero di infetti è massimo quando il numero di suscettibili
è pari a b/a.
TARATURA DEL MODELLO:
Per determinare completamente il modello (3,4) dell'epidemia
si devono valutare i parametri a
e b.
Stima di b
In assenza di suscettibili (x1=0),
gli infetti decrescono esponenzialmente:
| perché |
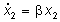 . . |
Pertanto, il periodo medio di incubazione T
è dato da:
e quindi b
è immediatamente calcolabile da T (che è assegnato).
Stima di a
Il numero di denunce d(t) rappresenta
il numero di individui che da infetti diventano immuni nel giorno t,
per cui:
Il numero di denunce d(t) può
quindi essere trasformato in numero di infetti x2(t)=Td(t).
In particolare è quindi noto lo stato iniziale del sistema:
Fissato a,
è pertanto possibile calcolare, con un opportuno package di simulazione,
l'evoluzione di x1(t) e x2(t)
a partire da queste condizioni iniziali e confrontare i valori così
calcolati di x2(t) nei giorni
t=7,10,11,12
con i dati Td(t) relativi agli stessi giorni.
Se i valori calcolati risultano errati, a
deve essere corretto e la simulazione ripetuta e così si deve procedere
finchè si trovi un valore di a
soddisfacente.
Per quanto riguarda la correzione da apportare ad
a,
si può notare che 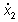 aumenta con a per
cui ad errori per difetto di x2(t)
devono corrispondere incrementi di a.
aumenta con a per
cui ad errori per difetto di x2(t)
devono corrispondere incrementi di a.
Stima dei costi di vaccinazione
Indicato con nv il numero
di vaccinati, il costo della campagna di vaccinazione risulta essere:
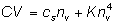 |
(5)
|
Il parametro K è facilmente stimabile
dato che si conoscono cs e il valore CV* di CV
per un numero di vaccinati pari a 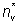 . .
MINIMIZZAZIONE
DEL COSTO SOCIALE:
Immaginando che la campagna di vaccinazione possa
essere eseguita con grande tempismo immediatamente dopo aver preso la decisione
al giorno t=12 e considerando questo istante come nuovo istante
iniziale t=0, abbiamo:
| x1(0)=N-Td(12)-nv |
(6)
|
| x2(0)=Td(12) |
(7)
|
Simulando il sistema (3,4) con queste condizioni
iniziali si determina l'evoluzione dell'epidemia conseguente ad un numero
di vaccinati pari a nv. In particolare
si può determinare:
che dipende da nv (mentre ,
vedi Fig.1). ,
vedi Fig.1).
Il costo di mancata produzione è dato da:
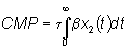 |
(8)
|
Poichè integrando le (3,4) tra 0 e 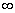 si ha
si ha
si può scrivere
per cui dalle (6,7,8) si ottiene:
Alternativamente, se il software usato permette di
simulare sistemi del terzo ordine, si può calcolare CMP aggiungendo
al sistema (3,4) una terza variabile di stato x3
con equazione di stato:
e condizioni iniziali x3(0)
nulle, così che (vedi(8)):
Il costo di vaccinazione CV è invece
direttamente calcolabile per mezzo della (5).
In conclusione, il costo sociale:
può essere calcolato per diversi valori di
nv
e il valore 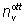 che minimizza Csoc può quindi
essere determinato numericamente con buona approssimazione.
che minimizza Csoc può quindi
essere determinato numericamente con buona approssimazione.
Poichè ogni valutazione di Csoc
richiede una simulazione, è bene che i valori nv
in corrispondenza dei quali si valuta Csoc
siano scelti con cura in modo da non dover eseguire un numero inutilmente
grande di simulazioni.

|