|
E’
chiaro che non essendo l’attività della compagnia saltuaria, occorre
determinare una soluzione periodica del problema e cioè una rotta
ciclica che colleghi varie città e che presenti il massimo rapporto
tra beneficio netto e tempi di percorrenza. Cercheremo quindi il ciclo
tra le varie città che presenta il massimo beneficio medio.
A
questo scopo è necessario definire quali siano i benefici netti
da associare alle rotte che collegano ciascuna coppia di città.
Consideriamo quindi due generiche città i e j che possono scambiarsi
Nij prodotti e definiamo il beneficio netto come la somma dei
ricavati qik(xk) ottenuti in j dalla vendita
dei prodotti meno i costi di acquisto in i dei prodotti stessi (pari al
prodotto delle quantità xk per i prezzi pik)
ed il costo del trasporto cij da i a j.
Risolveremo
dunque, per ogni coppia ij di città, il seguente problema
Nij con
i vincoli :
-capacità
di carico dell’aereo
Nij -non
negatività delle variabili di decisione
xk³ 0 k = 1,….,Nij Si
tratta di un classico problema di allocazione della capacità di
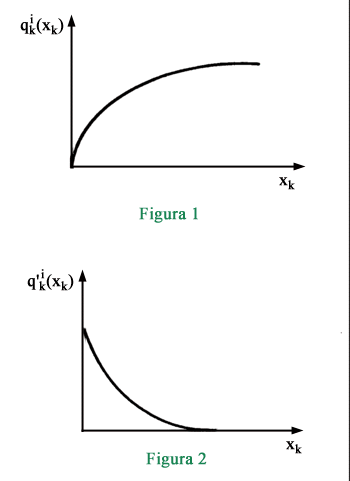
carico X disponibile tra i vari prodotti. Il problema è non lineare
a causa della non linearità dei benefici che di solito sono rappresentati
da curve del tipo di quelle illustrate in Fig. 1 e cioè crescenti
e concave. In questa ipotesi la curva del beneficio marginale q'k(xk)
è decrescente e convessa come in Fig. 2.
 Supponiamo dapprima che il vincolo sulla capacità totale sia attivo (cioè rappresenti all’ottimo un’uguaglianza), mentre siano non attivi i vincoli sulla non negatività delle variabili (il che è senz’altro accettabile date le ipotesi fatte sulle funzioni qjk(xk)). Utilizzando il metodo dei moltiplicatori di Lagrange, definiamo la funzione Nij Nij L(xk,l)
= å[qjk(xk)
- pikxk] - cij - l( åxk
- X)
K=1
k=1
le cui derivate rispetto a xk e a l uguagliate a zero forniscono il seguente sistema di Nij+1 equazioni algebriche q'jk(xk) - pik - l = 0 k = 1,……,Nij Tale
sistema può essere risolto molto semplicemente variando il valore
di l nelle
prime Nij equazioni, ricavando da ciascuna di esse il valore
di xk (si ricordi che i prezzi pik sono
noti) finchè non risulta soddisfatta anche l’ultima equazione. Dato
l’andamento monotono delle funzioni q'kj
(xk), a valori troppo bassi di l corrisponderanno
valori delle xk eccedenti la capacità di carico, mentre
valori alti del moltiplicatore faranno sì che la stessa non venga
pienamente utilizzata. Sarà dunque semplice modificare il valore
di l
( ad esempio con un algoritmo
di bisezione) fino ad ottenere la soluzione cercata. D’altra parte se il
vincolo sulla capacità non fosse stato attivo, l
sarebbe stato nullo e quindi le prime Nij equazioni avrebbero
direttamente fornito i valori cercati delle variabili xk.
Un
problema di questo tipo va risolto per ciascuna coppia ij di città
e naturalmente la soluzione del problema del trasporto da i a j differirà
da quella ottenuta tra j ed i. Al termine di questa procedura il grafo
da esaminare sarà costituito da coppie di archi con diverso orientamento
che collegano a due a due tutte le città e a ciascun arco sarà
associato un costo (o un beneficio) rij e un tempo tij.Su
questo grafo va individuato il ciclo a costo medio minimo (o equivalentemente
a ricavo medio massimo). Supporremo d’ora in poi che gli rij
indichino dei costi e pertanto siano negativi qualora su un certo percorso
prevalgano i benefici.
Per
giungere alla risoluzione del problema definiamo per ciascun arco un nuovo
costo r*ij dato da:
r*ij = rij - m tij e notiamo che se la somma lungo un ciclo G dei costi r*ij è minore di zero, ciò implica che il costo medio rGdel ciclo è minore di m, cioè: SG rij/SG tij < m e quindi anche il costo medio minimo r° è minore di m. D’altra parte per tutti i cicli per cui si verifica che la somma dei costi r*ij è positiva si può affermare che il relativo costo medio è superiore am. Sarà dunque possibile determinare il valore minimo di mcon un algoritmo che ne modifichi opportunamente il valore e verifichi, ad ogni passo, l’esistenza o meno di cicli lungo i quali la somma dei r*ij è negativa. L’algoritmo in questione può essere ancora un algoritmo di bisezione, ma può anche essere molto semplicemente una decrescita a scalini del valore di mfino alla scomparsa di cicli negativi. Occorre quindi, da ultimo, scegliere un opportuno metodo per individuare se nel grafo esistono cicli negativi. A questo scopo può essere usato l’algoritmo di programmazione dinamica che determina il cammino minimo tra due nodi qualunque di un grafo. Tale algoritmo, che è basato sull’assegnazione a ciascun nodo di un valore che rappresenta il minimo tra tutti i costi per raggiungere il nodo stesso da tutti quelli che lo precedono, raggiunge una soluzione (vale a dire il valore assegnato al nodo non viene più modificato) in un numero di passi al più pari al numero dei nodi. Nel caso ciò non si verifichi e quindi i valori assegnati ai nodi continuino a diminuire, ciò significa che nel grafo esiste almeno un ciclo a costo negativo. La soluzione del problema complessivo potrà dunque essere ottenuta con i seguenti passi: - soluzione, per ogni coppia (i,j) di città, di un problema (non lineare) di allocazione, che per la sua particolare struttura può essere ricondotta ad una ricerca monodimensionale sul moltiplicatore di Lagrange. In questo modo si determinano i pesi rij da assegnare agli archi del grafo. - soluzione del problema di ricerca del ciclo a costo medio minimo sul grafo definito dai costi rij. Per la soluzione di questo problema si può procedere nuovamente ad una ricerca monodimensionale sul valore ottimo del costo, utilizzando per ogni nuovo tentativo l’algoritmo dei cammini minimi per determinare la presenza o meno di cicli negativi. |