|
Dalle
ipotesi fatte segue che le funzioni
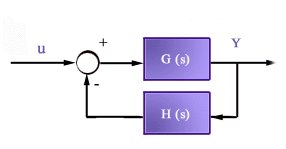
di trasferimento dei singoli componenti sono quelle Indicate nel seguente
schema a blocchi
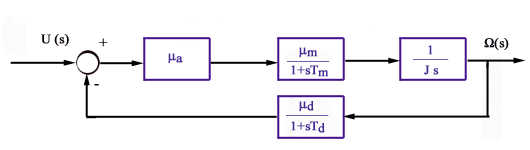 per cui la funzione dl trasferimento del sistema risulta data da
dove
Il sistema
è stabile se i poli
(le radici del denominatore) della funzione di trasferimento hanno parte
reale negativa. Per determinare sotto che condizioni ciò si verifica,
si deve quindi esaminare il segno delle radici del polinomio
Per
questo, posto D(s)
=a0s3+a1s2+a2s+a3,
si può applicare il metodo di Hurwitz alla matrice
La prima condizione di Hurwitz (a1> 0) è sempre soddisfatta perché dinamo e motore hanno ovviamente costanti di tempo positive. La seconda condizione di Hurwitz (a1a2 – a0a3>0) è invece soddisfatte se
Infine, la terza condizione (det(C)>0) è sempre soddisfatta nel caso la seconda lo sia. Ricordando l’espressione di K si può concludere pertanto che il sistema è esternamente stabile purché il guadagno dell’amplificatore non sia troppo elevato, cioè
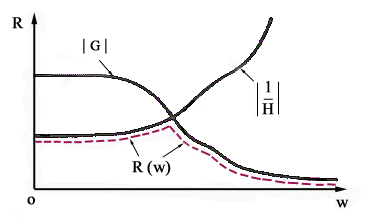
Per calcolare la banda passante del sistema è necessario determinare la sua risposta in frequenza, o meglio la funzione R(w) che definisce il rapporto tra le ampiezze delle sinusoidi di uscita e di ingresso. A tale scopo si possono usare i diagrammi di Bode che, pur essendo approssimati, forniscono buoni risultati e permettono di calcolare rapidamente la banda passante dl un sistema reazionato caratterizzato da una funzione di trasferimento G(s) in linea di andata e da una funzione di trasferimento C(s) in retroazione (vedi figura). Infatti la funzione di trasferimento del sistema è data da per
cui in prima approssimazione si ha
ciò
corrisponde a dire (vedi figura) che
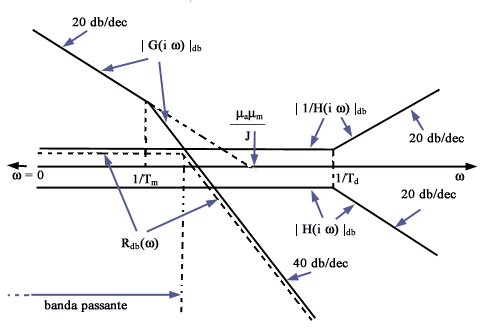
Nel caso specifico qui esaminato per cui il diagramma di Rdb(w) si ottiene con la costruzione illustrata in figura
La
banda passante del sistema è così facilmente individuabile
come la pulsazione cui avviene il primo cambiamento di pendenza del diagramma
di Rdb(w)
(in questo caso tale pulsazione è determinata dall’intersezione
di |
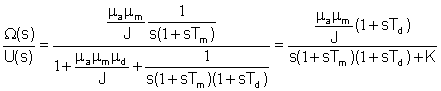
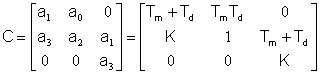
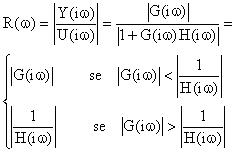 (1)
(1)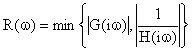 (2)
(2)