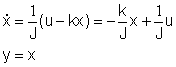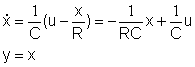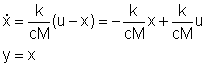Si consideri la relazione che intercorre tra la coppia u(t) esercitata da un motore su una massa rotante e la velocità angolare x(t) della massa stessa. In questo caso abbiamo

dove J è il momento d’inerzia e k il coefficiente di attrito viscoso, per cui i parametri m e T del sistema sono

m=1/k          T=J/k.

Quindi, al crescere del coefficiente di attrito k decrescono sia la velocità di regime della massa rotante che il tempo necessario per portarsi “praticamente” a regime.

Il momento d’inerzia J non influenza invece la velocità di regime ma solo la rapidità dei transitori.

Esempio elettrico

Si consideri il circuito R - C di figura 

descritto dalle equazioni

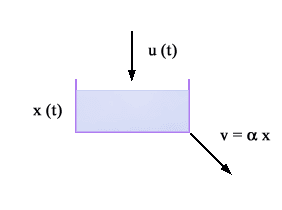
Tale circuito ha guadagno e costante di tempo dati da

m=R             T=RC

e questo evidenzia che la capacità del condensatore influenza soltanto i tempi di risposta del circuito.

Esempio idraulico

Il serbatoio (di sezione pari ed A) rappresentato in figura  è una costante dl tempo

Infatti, il serbatoio è descritto dalle equazioni

per cui

m=1                  T=A/a

In questo sistema il guadagno è unitario perché a regime la portata d’uscita è uguale a quella d’ingresso. La costante di tempo invece è più grande nei serbatoi di grande sezione o in quelli in cui la portata di uscita è poco sensibile alle variazioni di livello (apiccola).

Esempio termico

Si consideri il recipiente rappresentato in figura, con tenente una quantità M (in massa) di un materiale di capacità termica c. Detta u(t) la temperatura esterna e x(t) quella interna, si ha

dove k è la costante che regola lo scambio termico tra esterno ed interno (proporzionale allo sbalzo di temperatura (u - x)).

In questo caso si ha pertanto

m=1          T=cM/k

Il guadagno è unitario perché a regime temperatura interna ed esterna sono uguali. Per avere transitori rapidi è pertanto necessario avere materiali di bassa capacità ed usare grandi superfici di scambio (k elevato).

Esempio biologico

Una comunità di insetti nocivi vive su un’area dl superficie S ed ha densità pari a x(t). Tale comunità è caratterizzata da un coefficiente di riproduttività r e da uno di mortalità m e a basse densità tali coefficienti sono costanti e r>m. Infine, alcuni animali vengono eliminati per mezzo di insetticidi ad un tasso u(t).Con queste ipotesi e supponendo che u(t) sia tale da garantire che x(t) rimanga sempre sufficientemente basso, si ha

y=Sx      (= numero di animali)

Pertanto, in questo caso

Va notato che la costante di tempo T è in questo caso negativa e ciò rivela l’instabilità del sistema. Il guadagno è il rapporto tra numero di insetti e tasso di estinzione all‘equilibrio, ma tale equilibrio è instabile e non si può pertanto osservare in pratica. Ciò significa gli insetti si estinguono se (infatti, in questo caso) o aumentano indefinitamente nel caso contrario (naturalmente ciò è vero finché il modello è rappresentativo della realtà, cioè finché le densità x(t) non sono così elevate da far intervenire fenomeni come limitazione del cibo e dello spazio vitale, propagazione di epidemie, ecc, che si possono rappresentare soltanto con modelli non lineari).

Esempio economico

Un ente pubblico ha un capitale x(t) soggetto ad un interesse fisso i. Per statuto tale ente finanzia attività culturali di varia natura ad un tasso proporzionale al capitale x(t). Tutte le altre attività dell'ente (entrate o uscite) aumentano o diminuiscono il capitale ad un tasso u(t). Sotto queste condizioni, se la variabile di uscita y(t) è il capitale, si può scrivere

per cui si ha

In questo caso guadagno e costante di tempo sono uguali e il sistema è stabile se k>i, cioè se il tasso di investimento in attività culturali (k x(t)) supera il tasso di interesse (i x(t)).