Costi servizio di distribuzione: SOLUZIONE
E’ necessario cercare il valore di x, con 0 £x£ 5, che rende minima la funzione f(x).


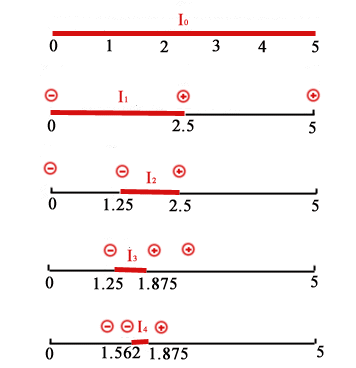
Per far questo saranno usati quattro diversi metodi, i quali partono da un intervallo di incertezza iniziale I0 (nel caso in esame l’intervallo [0,5]) e lo restringono, attraverso successive iterazioni, fino ad ottenere un intervallo di incertezza finale In minore della tolleranza consentita. Nei primi tre metodi (bisezione, sezione aurea, Fibonacci) l’intervallo d’incertezza finale è funzione unicamente di I0 e del numero di iterazioni, che è perciò determinabile a priori; nel quarto (interpolazione parabolica) l’intervallo di incertezza finale dipende anche dalla particolare funzione in esame.
 

BISEZIONE:

Ad ogni iterazione l’intervallo di incertezza si dimezza. Dopo n iterazioni si ha pertanto

In= I0 / 2n = 5 / 2n
Poiché In risulta minore di 0.4 per n ³ 4, sono necessarie 4 iterazioni, ognuna delle quali implica una valutazione della derivata f’(x), equivalente a 2 della funzione f(x). Poiché per inizializzare il metodo è necessario valutare la derivata negli estremi, il numero complessivo di valutazioni di f’(x) è 4+2=6, il che equivale a 12 valutazioni di f(x). L’intervallo di incertezza finale sarà
I4 = 5 / 24 = 0.3125
Nel caso in esame la derivata è disponibile in forma analitica e vale f’(x)=3x2-2x-5. Si eseguono i seguenti passi (Fig. 1):
 
inizializzazione: si valuta f’(x) negli estremi
f’(0) = -5 <0
f’(5) = 60 >0
1a iterazione: si valuta f’(x) nel punto x = 2.5 (punto di mezzo dell’intervallo [0,5])
f’(2.5) = 8.75 > 0
Poiché la derivata è negativa per x=0 e positiva per x=2.5, ai fini della ricerca del minimo viene selezionato l’intervallo I1=[0,2.5].
2a iterazione : f’(l.25) = -2.8125 < 0 
                         I2 = [1.25,2.5]
3a iterazione : f’(l.875) = 1.7969 > 0 
                         I3 = [1.25,1.875]
4a iterazione : f’(l.5625) = -0.8008 < 0 
                         I4 = [l.5625,l.875]

SEZIONE AUREA:

Ad ogni iterazione l’intervallo di incertezza si restringe riducendosi di circa il 38%

In = 0.62 In-1 = 0.62n I0
Poiché In risulta minore o uguale a 0.4 per n³ 6, è necessario effettuare 6 iterazioni, equivalenti a 9 valutazioni della funzione f(x): 2 valutazioni negli estremi (inizializzazione), 2 valutazioni alla prima iterazione (per posizionare 2 punti interni a I0), una valutazione ad ogni successiva iterazione. L’intervallo di incertezza finale è
I6 = (0 62)6 * 5 = 0.2835 <0.4
I passi da eseguire sono i seguenti (Fig. 2):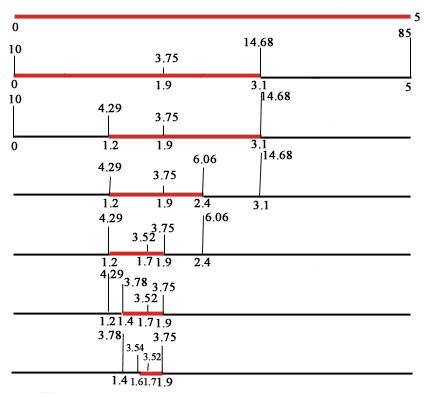

inizializzazione: si valuta f(x) negli estremi

f(0) = 10
f(5) = 85
1a iterazione: si posizionano secondo la sezione aurea i primi due punti interni a I0, che risultano essere x1=1.9 e x2=3.1 e si valuta in essi la funzione f(x)
f(x1) = 3.749
f(x2) = 14.681
Poiché f(x1) < f(x2), viene selezionato il nuovo intervallo di incertezza I1=[0,3.1].

2a iterazione: è necessario posizionare un ulteriore punto interno, che risulta essere x3=1.2. Poiché si ha f(1.2)=4.288 e quindi f(x1) < f(x3), viene selezionato il nuovo intervallo di incertezza I2=[1.2,3.1]

3a iterazione: x4 = 2.4 f(2.4) = 6.064 I3 = [1.2,2.4]
4a iterazione: x5 = 1.7 f(1.7) = 3.523 I5 = [1.2,1.9]
5a iterazione: x6 = 1.4 f(1.4) = 3.784 I6 = [1.4,1.9]
6a iterazione: x7 = 1.6 f(1.6) = 3.536 I7 = [1.6,1.9]
 

FIBONACCI:

L’intervallo di incertezza finale In è dato dalla relazione

In =I0 /Fn
dove I0 è l’intervallo d’incertezza iniziale e Fn è l’ennesimo numero di Fibonacci (F0=1, F1=1,...,Fi=Fi-1+Fi-2,...). Dato I0 = 5, si ha In £ 0.4 se Fn+1³12.5: è pertanto necessario effettuare un numero di iterazioni n = 5, equivalente a 8 valutazioni della funzione f(x). L’intervallo d’incertezza finale risulta essere
I5 = 5/13 = 0.3846 < 0.4
I passi da eseguire sono i seguenti:

inizializzazione: si valuta la funzione negli estremi: f(0) = 10 e f(5)=85.

1a e 2a iterazione: si posizionano i primi due punti interni x1 e x2 a distanza

5 (F5/ F6) = 3.077
rispettivamente da a e da b. Si ha x1=3.077, da cui f(x1)=14.28 e x2=1.923 da cui f(x2)=3.79. Poiché f(x1)>f(x2), si seleziona il nuovo intervallo di incertezza I1=[0,3.077].

3a iterazione: si posiziona il punto x3 simmetricamente a x2 nell’intervallo I1 ottenendo x3=1.154 da cui f(x3)=4.435. Poiché risulta f(x3)>f(x2) si seleziona il nuovo intervallo di incertezza I2=[1.154,3.077].

4a iterazione: x4=2.308 f(2.308) = 5.427 I3 = [1.154,2.308]
5a iterazione: x5=1.539 f(1.539) = 3.581 I4 = [1.154,1.923]
6a iterazione: x6=1.538 f(1.538) = 3.582 I5 = [1.538,1.923]

Si noti che gli ultimi due punti in cui è stata valutata la funzione (x5 e x6) distano tra loro di 0.001 solo per questioni di arrotondamento: in teoria essi sono posti a metà dell’intervallo di incertezza In-1 a distanza molto piccola l’uno dall’altro.
 

INTERPOLAZIONE PARABOLICA:

In questo caso l’intervallo di incertezza finale non è determinabile a priori.

1a iterazione: è necessario valutare la funzione in tre punti, ad esempio i due estremi e il punto medio dell’intervallo iniziale, individuare la parabola che passa per i 3 valori di f(x) così determinati e cercarne il minimo.

Si ha:

f(0)=10; f(5)=85; f(2.5)=6.875.
L’equazione di una generica parabola è
p(x) =ax2+bx+c
da cui
x=0 ®10=c
x=5 ®85=25a+5b+c
x=2.5 ®6.875=6.25a+2.5b+c
I coefficienti della parabola cercata sono:
a=6.5; b=-17.5; c=10.
Il nuovo punto in cui la funzione f(x) va valutata è il punto di minimo della parabola: si ha x=1.346 e f(1.346)=3.897.

A questo punto si scarta il valore più alto tra i 4 finora ottenuti, cioè quello corrispondente a x=5, e l’intervallo di incertezza risulta [0,2.5].

2a iterazione: l’equazione della nuova parabola si ottiene risolvendo il seguente sistema:

x=0 ®10=c
x=2.5 ®6.875=6.25a+2.5b+c
x=1.346 ®3.897=1.811a+1.346b+c
I coefficienti della parabola cercata sono:
a=2.84; b=-8.36; c=10.
Il nuovo punto in cui la funzione f(x) va valutata è il punto di minimo della parabola: si ha x=1.470 e f(1.470)=3.666.

Scartando il valore più alto tra i 4 valori correnti, cioè quello corrispondente a x=0, si ottiene il nuovo intervallo di incertezza [1.346,2.5].

Le successive iterazioni e il calcolo dell’intervallo di incertezza finale sono lasciati al lettore che ne fosse interessato.

Si noti che la convergenza di questo metodo è molto più rapida rispetto ai tre precedenti (cioè l’intervallo di incertezza si restringe molto più rapidamente), ma ogni iterazione richiede la risoluzione di un sistema di tre equazioni per determinare la parabola interpolante.

ESERCIZIO PRECEDENTE
Testo
  ESERCIZIO SUCCESSIVO