|
Indicato
con xi(t) il numero di animali di età i nell’anno t,
si ha
 per
cui la dinamica della comunità risulta descritta da un sistema lineare
discreto senza ingressi x(t+1) = A x(t) con matrice A data da
Gli
autovalori di questa matrice sono
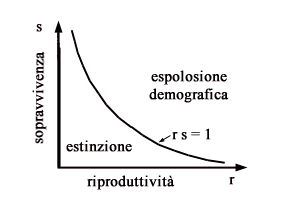
per cui il sistema risulta asintoticamente stabile se rs<1 e instabile se rs>1. Nel primo caso si ha la estinzione della specie (x1(t) e x2(t) tendono asintoticamente a zero), mentre nel secondo caso si ha una vera e propria esplosione demografica (x1(t) e x2(t) tendono all’infinito purché x1(0)>0). Il risultato è sinteticamente rappresentato in figura nello spazio dei parametri.
Per descrivere la dinamica di una comunità che non sia in fase di sviluppo indefinito o di estinzione è pertanto necessario che valga la relazione rs=1, cioè è necessario che i coefficienti di sopravvivenza e riproduttività siano tra loro ben bilanciati. In quest’ultimo caso i due autovalori sono sulla frontiera del cerchio di raggio unitario ed il sistema è semplicemente stabile. Gli stati di equilibrio sono infiniti (retta di equazione x2 = s x1 nel piano di stato) e qualora lo stato iniziale x(0) non sia una di questi stati di equilibrio, si ottiene un movimento periodico di periodo pari alla età massima dell’animale (infatti x(2) = A2 x(0)=x(0) perché A2 = I se rs = 1). |