|
Se
si indicano con L1 e L2 le superfici del due laghi
e con x1 e x2 i corrispondenti livelli, per il principio
di conservazione della massa si ottiene
dove
si è supposto L1 indipendente da x1 e L2
indipendente da x2.
Le
portate y1(t) e y2(t) non sono tuttavia variabili
indipendenti: esse sono in effetti univocamente legate ai livelli x1
e x2 secondo una legge (in generale non lineare) che dipende
dalla conformazione dell'emissario. In altre parole, si ha
e una tipica
funzione Sostituendo la (2) nella (1) e supponendo che cioè
supponendo che siano trascurabili i ritardi di propagazione, si ottiene
Il
modello è quindi costituito da un sistema non lineare del secondo
ordine con un ingresso (u1) ed una uscita (y2). Come
prima cosa determiniamo stato ed uscita di equilibrio corrispondenti ad
una portata di alimentazione costante u1. Poiché
all'equilibrio deve essere
si ottiene: che
è un sistema di due equazioni in due incognite facilmente risolubili.
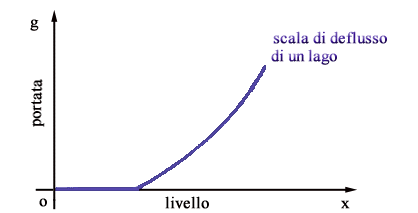
Se le scale di deflusso sono assegnate e graficamente il procedimento
è immediato: si riporta u1 sull'asse delle portate
delle scale di deflusso e si leggono i livelli x1 e x2
corrispondenti.
E'
ora importante chiedersi se sia ragionevole linearizzare il sistema nell’intorno
di uno stato di equilibrio oppure no. In altre parole è importante
fare l’analisi del sistema linearizzato e verificare se si è in
uno dei casi critici (casi in cui non mi può dedurre nessuna proprietà
del sistema dall’analisi del sistema linearizzato). Per questo si ricorda
che in un sistema del tipo
Il
sistema linearizzato associato ad uno stata di equilibrio x è
dato da
dove
dove
Il
sistema lineare (A, b, c’) così ottenuto è dato da
La
matrice A è in forma triangolare e pertanto i termini sulla diagonale
coincidono con gli autovalori, cioè
Poiché
questi autovalori sono negativi il sistema linearizzato è asintoticamente
stabile. Non siamo cioè in un caso critico e l'asintotica
stabilità del sistema linearizzato permette di concludere che
lo stato di equilibrio (x1, x2) corrispondente
all'ingresso costante u, è asintoticamente stabile. Ciò
è d’altra parte in pieno accordo con l’intuizione fisica che afferma
che variando di poco il livello dei due laghi (prelevando o immettendo
nel laghi stessi una piccola quantità d’acqua) si ottengono movimenti
perturbati che tornano nelle condizioni di equilibrio (x1,
x2).
E’
ora possibile eseguire una rapida analisi di raggiungibilità ed
osservabilità. Per quanto riguarda la raggiungibilità si
ha
che
è di rango massimo. Il sistema è, quindi, completamente
raggiungibile e ciò significa che (nell’ambito della validità
della linearizzazione) è possibile portare i due laghi ad un voluto
livello (
che
è anch'essa di rango massimo. Il sistema è, quindi, completamente
osservabile e ciò implica (sempre nell’ambito della validità
della linearizzazione) che è possibile risalire al valore dello
stato (x1, x2)(cioè ai livelli dei due laghi)
elaborando opportunamente le misure effettuate sulle sole portate u1(t)
e y2(t) (naturalmente non stupisce che da y2(t) si
possa determinare x2(t) poiché
Poiché
il sistema linearizzato è completamente raggiungibile e osservabile
la funzione
di trasferimento G(s) avrà denominatore di secondo grado. Risulta,
infatti,
dove
le costanti di tempo T1 e T2 sono date da:
Ovviamente, la funzione di trasferimento G(s) è il prodotto delle due funzioni di trasferimento G1(s) e G2(s) che rappresenta i due laghi in cascata (vedi figura). Dalle
espressioni delle costanti di tempo si nota che a grandi laghi corrispondono
(a parità di scale di deflusso) grandi costanti di tempo
(ad esempio una decina di giorni per il lago di Como e per il lago Maggiore
e qualche giorno per i laghi della Brianza). Laghi con scala di deflusso
molto ripida (g’ grande), cioè laghi con emissario tale che a piccole
variazioni di livello corrispondano grandi variazioni di portata, sono
caratterizzati da piccole costanti di tempo. In ultima analisi, quindi,
un lago esercita una funzione filtrante sulle variazioni della portata
di ingresso (si ricordi che la “costante di tempo” Soluzione del problema 1 Il primo problema posto è quello del calcolo del transitorio di uscita corrispondente alla rottura della diga che chiude il bacino di raccolta. A questo evento corrisponde ovviamente una brusca variazione della portata di ingresso u1 dal valore nominale u1 come mostrato in figura. La funzione è,
quindi, schematizzabile con un impulso di area opportuna dU
(si pensi che la durata del fenomeno è di pochi minuti) e, pertanto,
il problema posto può essere risolto calcolando la risposta all’impulso
del sistema, cioè
e
moltiplicandola per l'ampiezza dU
dell’impulso ottenendo così dy2.
Un calcolo approssimata di tale funzione può essere fatto ricordando
che la risposta all’impulso è l'antitrasformata della funzione di
trasferimento G(s). Si ottiene, pertanto,
e
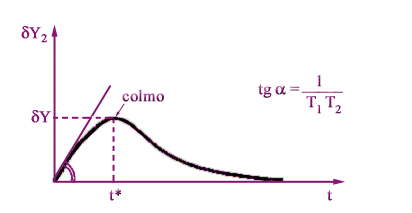
da queste tre condizioni si ricava che l'oscillogramma della variazione
della portata di uscita dy2
è
del tipo di quello mostrato in figura.
Per questo si pone (sviluppo di Heavyside) per
cui si ottiene
da
cui si ricava
Antitrasformando
secondo Laplace si ottiene allora
e
cioè
Derivando
questa espressione si ottiene
da
cui si può ricavare t* imponendo
e
cioè
Poiché
è
così immediato ricavare la portata al colmo
Il
secondo problema posto è quello del calcolo della portata di uscita Questa
formula si semplifica se si suppone che all’istante iniziale la stato del
sistema sia lo stato di equilibrio (x1, x2)
perché allora,
dove
Come
caso particolare di un certo interesse si consideri quello in cui
Dalla relazione segue
allora che
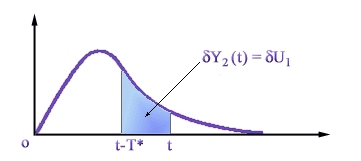
e cioè dy2(t) è proporzionale secondo il coefficiente dU1 all’area sottesa della risposta all’impulso del sistema nell’intervallo [t—T*, t] come mostrato in figura Nel
caso Questo
metodo non è però vantaggioso rispetto a quello precedentemente
esposto perché richiede la trasformazione
Terzo problema qui analizzato è quello dell’effetto che lo scioglimento delle nevi. ha sulla portata di uscita del secondo lago. In periodo di scioglimento delle nevi la portata di alimentazione risulta periodicamente variabile con periodo T=1 [giorno], cioè u1(t)=u1(t+T) "t. A tale funzione periodica di ingresso corrisponde un’unica funzione periodica di uscita (questo risultato è scontato dal punto di vista intuitivo); nell’ipotesi che la portata di ingresso u1(t) sia, in prima approssimazione di tipo sinusoidale, e cioè u1(t) = u1+d sen(wt) w = 2p/T è
allora interessante calcolare l'ampiezza dY2
della corrispondente sinusoide dy2(×)
(che dy2(×)
sia una sinusoide è vero soltanto nel caso in cui sia lecito descrivere
il fenomeno dinamico in esame per mezzo del sistema linearizzato). Il calcolo
di dY2
può
essere effettuato facendo ricorso al concetto di “risposta in frequenza”
che afferma che il rapporto tra le ampiezze delle sinusoidi in uscita e
in ingresso è pari al modulo della funzione di trasferimento valutata
per s=iw.
Nel caso in esame si ha allora
E’ evidente, allora, che qualora T<Ti i =1,2 si
ha una forte “attenuazione” nel senso che
dY2 << dU1 I
laghi operano cioè come veri e propri filtri passa basso e
la variazione giornaliera di portata di alimentazione non dà praticamente
alcun effetto sulla portata dell’ultimo emissario. Un calcolo approssimato
dell’attenuazione introdotta dal sistema si può eseguire per mezzo
del semplice diagramma di Bode riportato in figura.
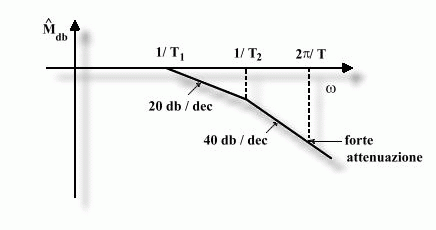
Dal
diagramma si vede come la banda passante del sistema coincida con l’inverso
della più grande costante di tempo. Variazioni periodiche dell’ingresso
corrispondenti a pulsazioni w<1/T1
si ritrovano inalterate all’uscita del sistema, mentre le variazioni a
frequenza più elevata vengono attenuate (filtrate).
|

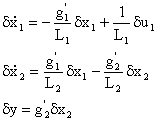


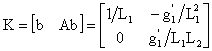
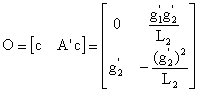
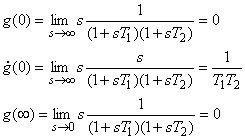
.gif)