|
Poiché
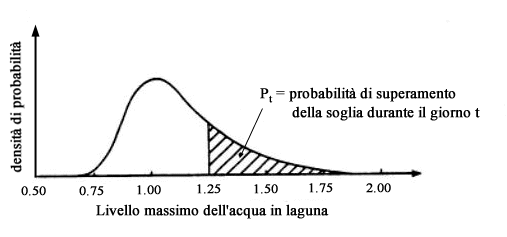
ogni giorno t il modello fornisce la distribuzione del massimo livello
in Laguna tra le ore 8.00 e le ore 24.00, si può facilmente calcolare
, con la semplice operazione di integrazione mostrata in figura, la probabilità
pt che in tale periodo il livello dell’acqua superi il valore
di soglia x* = 1.25.
E’
pertanto logico decidere di dare l’allarme quando la probabilità
pt è grande e non darlo quando invece tale probabilità
è bassa. Il problema è quindi quello di determinare il valore
p* di probabilità con cui discriminare tra probabilità elevate
e probabilità basse (non è detto a priori che il valore p*
= 0.5 sia quello da scegliere).
Per
questo si può usare il modello per un periodo di prova e costruire
così una tabella come quella riportata di seguito che fa riferimento
a un ipotetico periodo di prova di 20 giorni (venti colonne).
Nella prima riga della tabella sono riportati i livelli massimi raggiunti durante il giorno, mentre in seconda riga è riportato il valore della probabilità pt di superamento della soglia calcolata a partire dall’informazione fornita dal modello secondo la procedura illustrata nella figura. Nelle rimanenti quattro righe della tabella sono riportate le decisioni che si sarebbero prese con quattro valori diversi e crescenti della probabilità p*. Se pt³ p* la decisione è di dare l’allarme e in tabella compare quindi un sì. In caso opposto (pt< p*) compare un no. Poiché i valori di p* sono crescenti di riga in riga (da 0.4 a 0.7), ogni sì avrà nella stessa colonna altri sì nelle righe precedenti (pt³0.5 implica pt> 0.4) e ogni no avrà invece altri no nelle righe seguenti (pt< 0.5 implica pt< 0.6 e pt< 0.7). Si
può allora esaminare la tabella colonna per colonna e contare così
il numero di falsi allarmi (cerchi) e di mancati allarmi (quadrati).
Ad
esempio, la prima colonna corrisponde ad un giorno in cui il livello non
supera il livello di soglia (1.23 <
1.25) per cui l’allarme non dovrebbe essere dato: nella riga p* = 0.4 compare
invece un sì che è quindi un falso allarme. In seconda
colonna non si hanno né falsi allarmi né mancati allarmi
perché sì. è la risposta esatta. Nella terza
colonna abbiamo invece due mancati allarmi (i no delle righe p*
= 0.6 e p* = 0.7). Procedendo a questo modo si perviene alla seguente tabella
che mostra come all’aumentare della probabilità p* diminuiscano
i falsi allarmi e aumentino i mancati allarmi.
Il valore ottimo di p* (tra quelli esaminati) dipende quindi dai pesi relativi che si vogliono dare ai due possibili errori. Se, ad esempio, il danno (o il disagio) generato da un mancato allarme viene ritenuto doppio di quello che si ha in caso di falso allarme, la soluzione migliore è quella con p* = 0.5; ma se, invece, il danno per mancato allarme è dieci volte più grande di quello per falso allarme, allora la migliore soluzione è p* = 0.4. E’ ovvio che per ottenere un risultato più significativo, la procedura qui descritta debba essere applicata ad un insieme di dati sufficientemente numeroso e rappresentativo e che la discretizzazione della variabile p* (di per sé continua) debba essere più fitta di quella qui esaminata. |