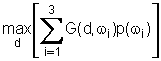|
Per
risolvere il problema si deve innanzitutto costruire la tabella dei guadagni
G(d,w)
sottraendo i costi dai ricavi:
La massimizzazione del guadagno aspettato consiste quindi nel risolvere il problema Poiché
p(wi)
= 1/3 per i=1, 2, 3, in pratica si deve effettuare la somma per righe degli
elementi della tabella dei guadagni e scegliere la riga a somma massima.
Nel caso specifico lo schema prescelto è quindi d2.
Se
il decisore è pessimista il suo criterio di scelta sarà
Ciò
significa fissare l’attenzione sull’elemento minimo di ogni riga e scegliere
poi la riga cui corrisponde il massimo di questi elementi. Nel caso specifico
dato che gli elementi minimi di ogni riga sono quelli dell’ultima colonna,
il problema si risolve determinando il massimo di questa colonna (-5).
La soluzione è pertanto lo schema pubblicitario d1.
Se
il decisore è ottimista il suo criterio di scelta sarà
In
questo caso quindi si determina il massimo elemento di ogni riga e quindi
il massimo tra questi elementi, il che equivale a scegliere il massimo
assoluto della tabella. Nel caso specifico il massimo assoluto della tabella
(100) si ottiene con lo schema pubblicitario d3.
|