|
Si indichino con x1
il numero di borsette e con x2 il numero di paia di scarpe
prodotte settimanalmente. Il guadagno netto complessivo (funzione obiettivo
da massimizzare) è dato da
J(x1,x2) = 60 x1 + 30 x2.J è funzione di due variabili; è tuttavia possibile rappresentarne nel piano x1x2 le linee di livello, cioè le linee a guadagno costante. Posto J(x1,x2)=k, si ottiene, al variare di k, un fascio di rette parallele di coefficiente angolare m=-60/30=-2. Tutti i punti di una stessa retta corrispondono a un particolare valore del guadagno k; al crescere di k, ci si sposta su rette più lontane dall’origine. I vincoli sono i seguenti: 0.05x1 + 0.03x2£ 8 (massima quantità di pelle disponibile settimanalmente) 2x1 + 4x2£ 200 (massima quantità di manodopera disponibile settimanalmente) x1, x2³ 0 (vincolo di non negatività delle variabili)La regione di ammissibilità OAB determinata dai vincoli dati è mostrata in figura, insieme al fascio di rette che rappresenta le linee di livello della funzione obiettivo. Si noti che la regione OAB è determinata, oltre che dagli assi cartesiani, dal solo vincolo (2), che risulta sempre più restrittivo del vincolo (1). Ciò significa che, dato il vincolo sulla manodopera, la quantità di pelle disponibile non è un elemento a sua volta vincolante. La soluzione ottima del problema è data dal punto A, cioè dal punto della regione delle soluzioni ammissibili che corrisponde alla linea di livello più lontana dall’origine. 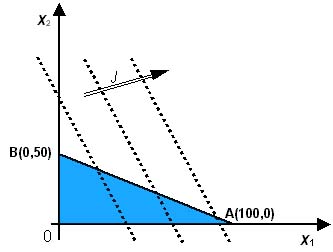
Le coordinate di A sono x1=100 e x2=0 : la soluzione ottima corrisponde pertanto a una produzione settimanale di 100 borsette e 0 paia di scarpe, con l’impiego di tutta la manodopera disponibile (200 unità) e di parte della pelle disponibile (5 quintali) e con un guadagno netto settimanale di 6 milioni di lire.
|