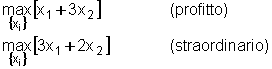|
Si
tratta di un problema a due obiettivi: massimizzazione del profitto e minimizzazione
del tempo di straordinario, che ovviamente risultano tra loro conflittuali.
Le
variabili di decisione sono le quantità x1 e x2
dei
due gelati da produrre e le due funzioni obiettivo sono date da:
I
vincoli del sistema sono costituiti dalle disponibilità di componenti
base e dalla non-negatività delle quantità prodotte. Quindi
2x1 + x2£ 32 Risolviamo
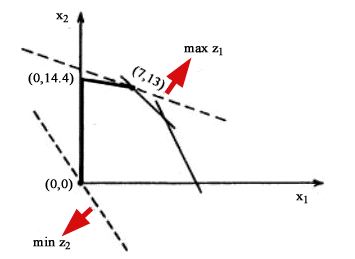
il problema geometricamente. Prima di tutto determiniamo la regione delle
soluzioni ammissibili nello spazio delle variabili di decisione. Essa è
riportata in Fig. 1.

Figura1 Per determinare le soluzioni efficienti possiamo applicare il metodo dei vincoli. Fissiamo quindi un certo valore K per il secondo obiettivo e otteniamo così un nuovo vincolo (vedi Fig. 2).
In corrispondenza di ciascun valore di K possiamo calcolare il massimo della prima funzione obiettivo e determinare così il tratto in grassetto in Fig. 2. Possiamo poi valutare su ciascun vertice (ricordiamo che in un caso lineare la soluzione ottima coincide sempre con uno dei vertici della regione di ammissibilità) le quantità z1 = x1 + 3x2 e
riportare la linea delle soluzioni efficienti nel piano degli obiettivi
(Fig. 3).
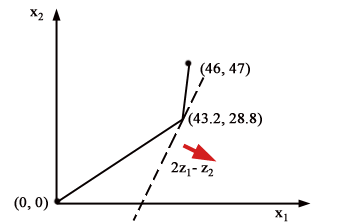
Figura 3 Date infine le curve di indifferenza della direzione generale, 2z1 - z2 = costante che
hanno l’inclinazione della retta tratteggiata in Fig. 3, la scelta finale
sarà costituita da x1 = 0, x2 = 14.4, punto
in cui la curva di indifferenza tocca l’insieme delle soluzioni efficienti.
|