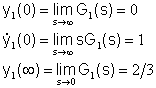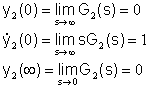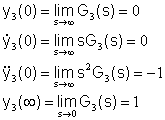|
Poiché
tutte e tre le funzioni
di trasferimento Gi(s) hanno poli
soltanto nel semipiano sinistro, si può applicare, oltre al teorema
del valore iniziale, anche quello del valore finale.
Nel primo
caso abbiamo
Poiché
i poli sono reali non si hanno oscillazioni e l’andamento qualitativo della
risposta
allo scalino è pertanto il seguente
 Per il
secondo sistema abbiamo invece
In questo
caso i poli sono complessi coniugati e quindi si. hanno oscillazioni smorzate
e la risposta allo scalino è la seguente (gli zeri sono ugualmente
intervallati)
Infine, per il terzo sistema abbiamo
per cui l’andamento qualitativo della risposta allo scalino (vi sono due poli complessi coniugati) è il seguente
|