|
La
scelta del progetto migliore è formalmente un problema di ottimizzazione
a molti obiettivi:
min [ rischio; -rendimento; costo ] La
soluzione può quindi dipendere dall’importanza relativa che si vuol
dare ai tre obiettivi.
Se
gli obiettivi fossero in ordine di importanza decrescente e ogni obiettivo
fosse ritenuto di gran lunga più importante del seguente, allora
la scelta si potrebbe fare col criterio lessicografico. Si determinerebbero
così innanzitutto i progetti a minimo rischio, che nel caso specifico
sono i progetti 2 e 3, cui corrispondono in media 0.2 incidenti mortali/anno.
Indi tra questi due progetti si sceglierebbe il 2 perché è
quello col rendimento più alto.
Se
gli obiettivi sono invece di importanza paragonabile, la soluzione deve
essere determinata scegliendo opportunamente tra le soluzioni “efficienti”.
Queste ultime si trovano paragonando fra loro i valori degli obiettivi
che compaiono nella tabella e scartando i progetti “dominati”. Tra i progetti
efficienti ci devono per forza essere quello a minimo rischio (il 2 o il
3), quello a massimo rendimento (il 5) e quello a minimo costo (il 7).
Nel caso specifico la soluzione 3 è dominata dalla 2, per cui questo
primo rapidissimo esame dei dati fornisce le soluzioni 2, 5 e 7 come certamente
non dominate. L’analisi dettagliata della tabella mostra che non esistono
altre soluzioni efficienti. Infatti, il progetto 1 è dominato dal
2 e dal 7, il 3 è (come già detto) dominato dal 2, il 4 è
dominato dal 7 e 6 e 8 sono dominati da 2. Il grafo completo delle dominanze
è riportato in Fig. 1, ove i progetti efficienti sono quelli che
corrispondono ai nodi da cui non escono archi (2, 5 e 7).
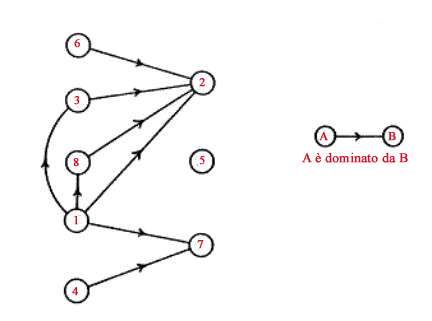
Figura 1 La
soluzione va quindi cercata tra quelle efficienti (2, 5, 7) eseguendo un’analisi
di compromesso tra gli obiettivi. Per questo usiamo il metodo dei pesi
che consiste appunto nell’assegnare dei pesi p1, p2,
p3 di importanza relativa ai singoli obiettivi. Non avendo dati
a disposizione eseguiamo l’analisi in termini parametrici e fissiamo a
priori p3=1. Inoltre esprimiamo il rischio J1 in
numero medio di incidenti mortali/anno, il rendimento J2 in
per cento e il costo J3 in miliardi di lire/anno (costo dell’impianto/durata
dell’impianto (20 anni)).
La funzione obiettivo da minimizzare sarà pertanto J = p1J1 - p2J2 + p3J3 dove il peso p1 rappresenta il valore (in miliardi di lire) attribuito ad una vita umana e il peso p2 rappresenta il surplus di guadagno annuo (sempre in miliardi di lire) dovuto ad un incremento dell’un per cento del rendimento dell’impianto. Per le tre soluzioni efficienti (2, 5 e 7) otteniamo allora J(2) =0.20 p1 - 70 p2+4.50 Uguagliando
a due a due queste espressioni otteniamo le equazioni di tre rette
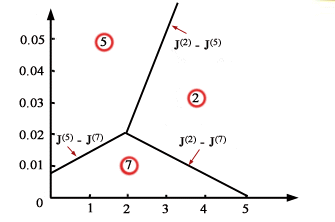
-0.35 p1 + 10 p2 + 0.50 = 0 J(2) = J(5) che rappresentano nel piano (p1 ,p2) le linee di indifferenza tra due progetti. Ad esempio, la retta J(2) = J(5) separa il piano (e, in particolare, il primo quadrante) in due regioni: una regione in cui il progetto 2 è preferibile al 5 e l’altra in cui accade il contrario. Di queste due regioni quella che contiene l’origine p1 = p2 = 0 è quella in cui è preferibile il progetto 5 che ha un costo (J3 = 4.00) inferiore al costo del progetto 2 (J3 = 4.50). Il primo quadrante del piano (p1 ,p2) viene così diviso in tre sottoregionicome mostrato in Fig. 2, in ognuna delle quali risulta migliore uno dei tre progetti.
Fissata
una coppia di valori (p1,p2) è così
immediato determinare quale è l’impianto da realizzare. La figura
mostra che se p1 è molto grande il progetto da scegliere
è il 2 (vedi criterio lessicografico). Se invece il valore attribuito
alla vita umana è (benché grande) limitato, il progetto da
scegliere può essere anche il 5 o il 7. Se, ad esempio, il surplus
di guadagno per ogni punto aggiuntivo di rendimento è pari a 300
milioni (p2=0.3) il progetto da scegliere è il 5, a meno
che il valore attribuito ad una vita umana sia superiore a 10 miliardi
di lire.
|