Testing for optimality involves using the reduced costs that were found in the previous step.
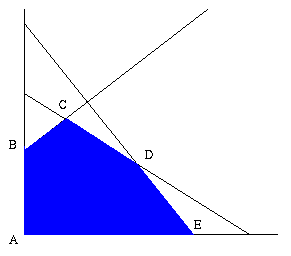
Consider figure 1.

Say we are at point D. The reduced costs tell us whether or not the solution will improve if we move from point D to point C or point E. If the reduced cost is negative, the solution will improve if we move from the current vertex to the next vertex. Algebraically this means that we remove one variable from the basis and replace it with another.
We know the current answer to the linear program is optimal if all the reduced costs are either zero or positive. There are no edges which we can traverse to increase the objective function. Remember that we are minimizing.
There are three possibilities if all the reduced costs are greater than or equal to zero.
1 If you are in phase 1 and the objective value is zero, remove the artificial variables from the problem and continue with step 3. You are now in phase 2.
2 If you are in phase 1 and the objective value is greater than zero, that means your linear program is infeasible. There is no solution.
3 If you are in phase 2, stop because you have found the optimal solution.
If there are variables with negative reduced costs, move on to the next step. Otherwise, you have solved the linear program because the solution at any of the other vertices will not improve the current solution.