The Simplex Method:
Step 3

Calculate the Reduced Costs.

It can be proven that the optimal solution to a linear program will occur at one of the vertices of the feasibility region. The feasibility region is the set of all points that satisfy the constraints. Consider Figure 1. Figure 1 shows the graph of the feasibility region for the the following constraints.

1. x₁+x₂ 3
2. x₁+2x₂ 4
3. -x₁+x₂ 1
4. x 0

Figure 1

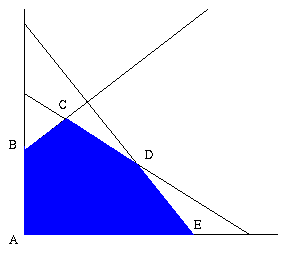
The optimal solution can be at points A, B, C, D, or E. Intuitively, the reduced costs indicate if there is an edge from the current vertex that we can traverse to improve the current solution. There can be many such edges.

The reduced costs are calculated by solving the system of equations pi^T B = c_B^T where c_B is the cost of the basic variables. Similarly you can calculate pi by solving B^T pi = c_B. The reduced costs for each nonbasic variable is then calculated by solving d = c - pi A_j where c is the cost of the nonbasic variable and the quantity pi A_j is the dot product of pi^T and the column of A. The pi vector is also referred to as the price vector. For those of you who know more about linear programming, the pi vector is the dual variables. The reduced costs are used in step 4 and step 5.

[ Indice spiegazione | Applet di calcolo | Torna indietro ]