Il movimento
libero 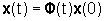 di un
sistema
lineare è completamente individuato dalla matrice di transizione
di un
sistema
lineare è completamente individuato dalla matrice di transizione

Tenendo presente quanto detto su autovettori,
autovalori e forma di Jordan di A, si può concludere che,
nel caso di autovalori reali e distinti, il movimento libero è del
tipo

dove x(i), i=1,…,n sono
gli autovettori di A (che soddisfano la relazione Ax(i)=lix(i)e
ci sono le componenti dello stato iniziale x(0) nella base individuata
dagli n autovettori (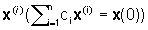 ).
Naturalmente per condizioni iniziali particolari qualche ci può
risultare nullo, ma per condizioni iniziali generiche tutti i ci sono diversi
da zero e il movimento libero è la somma pesata di n esponenziali
a tempo continuo o discreto. Al passare del tempo una di queste esponenziali
domina per forza tutte le altre perché per t grande ).
Naturalmente per condizioni iniziali particolari qualche ci può
risultare nullo, ma per condizioni iniziali generiche tutti i ci sono diversi
da zero e il movimento libero è la somma pesata di n esponenziali
a tempo continuo o discreto. Al passare del tempo una di queste esponenziali
domina per forza tutte le altre perché per t grande 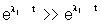 [
[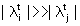 ] se ] se 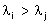 [
[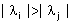 ] e ciò
accade sia nel caso di asintotica
stabilità ( ] e ciò
accade sia nel caso di asintotica
stabilità (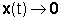 )
che nel caso di semplice stabilità o instabilità. L'autovalore
e l'autovettore corrispondenti a questa esponenziale sono chiamati dominanti.
L'autovalore dominante ldom
è
chiaramente l'autovalore massimo nel caso dei sistemi a tempo continuo
e l'autovalore a massimo modulo nel caso dei sistemi a tempo discreto.
La Fig. 9 riporta ben cinque casi ((b), (d), (e), (f), (g)) di sistemi
a tempo continuo con autovalori reali e mostra come per )
che nel caso di semplice stabilità o instabilità. L'autovalore
e l'autovettore corrispondenti a questa esponenziale sono chiamati dominanti.
L'autovalore dominante ldom
è
chiaramente l'autovalore massimo nel caso dei sistemi a tempo continuo
e l'autovalore a massimo modulo nel caso dei sistemi a tempo discreto.
La Fig. 9 riporta ben cinque casi ((b), (d), (e), (f), (g)) di sistemi
a tempo continuo con autovalori reali e mostra come per 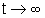 tutte le traiettorie generiche tendano ad allinearsi con l'autovettore
dominante. Questa proprietà è molto importante e va spesso
tenuta presente per caratterizzare il comportamento asintotico di un sistema
lineare. Il movimento libero è, quindi, approssimabile sui tempi
lunghi con una semplice esponenziale
tutte le traiettorie generiche tendano ad allinearsi con l'autovettore
dominante. Questa proprietà è molto importante e va spesso
tenuta presente per caratterizzare il comportamento asintotico di un sistema
lineare. Il movimento libero è, quindi, approssimabile sui tempi
lunghi con una semplice esponenziale

e se il sistema è asintoticamente
stabile l'esponenziale tende a zero. In questi casi è consuetudine
scrivere l'esponenziale (sia a tempo continuo che a tempo discreto) nella
forma 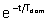 dove dove 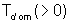 è la cosiddetta costante di tempo dominante, legata all'autovalore
dominante dalla relazione
è la cosiddetta costante di tempo dominante, legata all'autovalore
dominante dalla relazione

È poi prassi comune nelle applicazioni
ritenere che l'esponenziale sia "praticamente" esaurita dopo un periodo
di tempo pari a cinque volte la costante di tempo Tdom.
Se gli autovalori di A, pur essendo distinti,
non sono tutti reali, il movimento libero è anche caratterizzato
da termini del tipo elt
e lt
con l complesso.
Nel caso di tempo continuo tali termini corrispondono a funzioni sinusoidali
modulate esponenzialmente 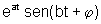 dove a è la parte reale dell'autovalore e b la parte immaginaria.
Ne segue che il termine dominante del movimento libero risulta essere quello
associato all'autovalore reale o alla coppia di auovalori complessi coniugati
con massima parte reale. In conclusione, quindi, sui tempi lunghi il movimento
libero è approssimabile con quello di un sistema del primo ordine
con autovalore pari a quello dominante o con quello di un sistema del secondo
ordine con autovalori complessi uguali a quelli dominanti. Nel primo caso
il movimento libero è del tipo esponenziale, mentre nel secondo
caso è una sinusoide di ampiezza variabile esponenzialmente. Naturalmente,
nel caso di sistemi a tempo continuo asintoticamente stabili la costante
di tempo dominante è data da
dove a è la parte reale dell'autovalore e b la parte immaginaria.
Ne segue che il termine dominante del movimento libero risulta essere quello
associato all'autovalore reale o alla coppia di auovalori complessi coniugati
con massima parte reale. In conclusione, quindi, sui tempi lunghi il movimento
libero è approssimabile con quello di un sistema del primo ordine
con autovalore pari a quello dominante o con quello di un sistema del secondo
ordine con autovalori complessi uguali a quelli dominanti. Nel primo caso
il movimento libero è del tipo esponenziale, mentre nel secondo
caso è una sinusoide di ampiezza variabile esponenzialmente. Naturalmente,
nel caso di sistemi a tempo continuo asintoticamente stabili la costante
di tempo dominante è data da
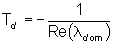
Infine se gli autovalori di A sono multipli,
il movimento libero può anche contenere termini del tipo tkelt
[tklt]
nel caso di sistemi a tempo continuo [discreto]; ciò non modifica
tuttavia le conclusioni già tratte, perché il movimento libero
continua ad essere dominato dal termine associato all'autovalore reale
o alla coppia di autovalori complessi coniugati con massima parte reale
[massimo modulo]. |


