È noto che in alcuni sistemi, come, ad esempio,
quelli elettrici e meccanici, è possibile definire una funzione
di stato 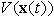 ,
detta energia, che ha la proprietà di essere quadratica e non negativa
e di decrescere nel tempo (tendendo a zero) qualora il sistema sia asintoticamente
stabile ed evolva liberamente. Queste proprietà, approfondite
dal matematico russo Alexander Liapunov (ormai più di un
secolo fa), permettono di analizzare il problema della stabilità
di tutti i sistemi lineari in modo estremamente sintetico ed elegante. ,
detta energia, che ha la proprietà di essere quadratica e non negativa
e di decrescere nel tempo (tendendo a zero) qualora il sistema sia asintoticamente
stabile ed evolva liberamente. Queste proprietà, approfondite
dal matematico russo Alexander Liapunov (ormai più di un
secolo fa), permettono di analizzare il problema della stabilità
di tutti i sistemi lineari in modo estremamente sintetico ed elegante.
Per presentare questa tematica premettiamo la definizione
di matrice definita positiva e alcune semplici considerazioni. Innanzitutto
diciamo che una funzione 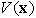 con
con 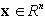 si dice
quadratica se si dice
quadratica se
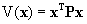
con P matrice 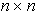 .
Ciò significa che .
Ciò significa che 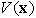 è una somma pesata di tutti i prodotti
è una somma pesata di tutti i prodotti 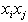 .
Poiché il peso del termine .
Poiché il peso del termine 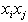 è (
è (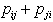 ) non
è limitante supporre che la matrice P sia simmetrica. Inoltre,
una matrice P si dice definita positiva se la forma quadratica ) non
è limitante supporre che la matrice P sia simmetrica. Inoltre,
una matrice P si dice definita positiva se la forma quadratica 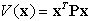 ad essa associata è positiva per tutti i vettori
ad essa associata è positiva per tutti i vettori 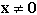 .
Per sapere se un'assegnata matrice P è definita positiva
si può applicare il seguente criterio. .
Per sapere se un'assegnata matrice P è definita positiva
si può applicare il seguente criterio.

Condizione necessaria e sufficiente perchè
una matrice simmetrica
P sia definita
positiva è che siano positivi tutti i suoi primi minori principali 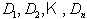 ,
cioè ,
cioè
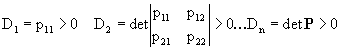
|
Da quanto detto è evidente che ogni
matrice P definita positiva induce una metrica nello spazio Rn
nel senso che 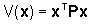 può essere interpretato come la distanza del punto x dall'origine.
In questa metrica, i punti x equidistanti dall'origine stanno su
varietà di equazione
può essere interpretato come la distanza del punto x dall'origine.
In questa metrica, i punti x equidistanti dall'origine stanno su
varietà di equazione 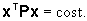 ,
che in R2 sono ellissi. ,
che in R2 sono ellissi.
Associamo allora ad un sistema lineare
autonomo a tempo continuo 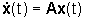 una matrice definita positiva P. La "distanza" dello stato x(t)
dall'origine è, pertanto,
una matrice definita positiva P. La "distanza" dello stato x(t)
dall'origine è, pertanto, 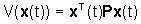 e tale distanza varia nel tempo poiché x dipende da t.
Più precisamente
e tale distanza varia nel tempo poiché x dipende da t.
Più precisamente
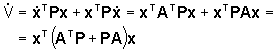
per cui la distanza di x(t) dall'origine
continuerà a diminuire nel tempo (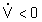 )
se la matrice )
se la matrice 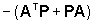 è definita positiva, cioè se è soddisfatta la cosiddetta
equazione
di Liapunov
è definita positiva, cioè se è soddisfatta la cosiddetta
equazione
di Liapunov
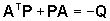 (25)
(25)
con Q definita positiva. Ovviamente,
se tale equazione è soddisfatta il sistema è asintoticamente
stabile perché il movimento
libero del sistema tende asintoticamente a zero dato che 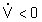 per
per 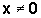 . .
Nel caso dei sistemi a tempo discreto 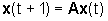 si deve, invece, determinare la variazione DV
della distanza V
si deve, invece, determinare la variazione DV
della distanza V
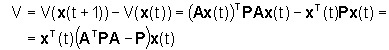
per cui l'equazione di Liapunov a tempo discreto
è
 (26)
(26)
In conclusione, se un sistema lineare a
tempo continuo [discreto] soddisfa l'equazione di Liapunov (25) [(26)]
con P e Q definite positive il sistema è asintoticamente
stabile e la funzione 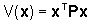 ,
detta funzione di Liapunov, ha le proprietà della funzione energia,
cioè è positiva e decrescente nel tempo per ,
detta funzione di Liapunov, ha le proprietà della funzione energia,
cioè è positiva e decrescente nel tempo per 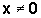 .
Ciò non significa naturalmente che in un sistema autonomo asintoticamente
stabile, in cui, quindi x(t) tende a 0 per .
Ciò non significa naturalmente che in un sistema autonomo asintoticamente
stabile, in cui, quindi x(t) tende a 0 per 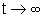 ,
qualsiasi funzione quadratica ,
qualsiasi funzione quadratica 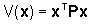 con P definita positiva, decresce sistematicamente nel tempo anche
se V tende a 0 per
con P definita positiva, decresce sistematicamente nel tempo anche
se V tende a 0 per 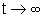 .
Questo fatto è illustrato in Fig. 11 per un sistema del secondo
ordine a tempo continuo (fuoco stabile). In tale sistema .
Questo fatto è illustrato in Fig. 11 per un sistema del secondo
ordine a tempo continuo (fuoco stabile). In tale sistema 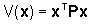 è definita positiva, ma
è definita positiva, ma 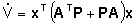 è in alcuni punti positiva e in altri negativa per cui V
tende a 0 per
è in alcuni punti positiva e in altri negativa per cui V
tende a 0 per 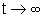 ma non monotonicamente.
ma non monotonicamente.
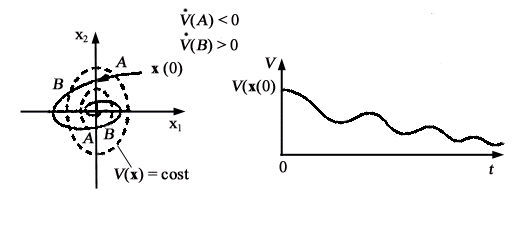
|
Figura 11 Sistema autonomo
asintoticamente stabile del secondo ordine (fuoco stabile):
(a) traiettoria (_____)
e linee di livello (.......) della funzione 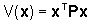 ;
(b) andamento di V nel tempo ;
(b) andamento di V nel tempo |
Quanto detto è riassunto e ulteriormente precisato
nel seguente teorema.
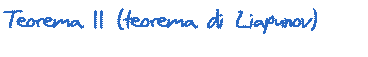
Un sistema lineare (A,-,-)
a tempo continuo [discreto] è
asintoticamente stabile se e solo se esiste una funzione quadratica 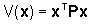 con P definita positiva che sia strettamente decrescente nel tempo
(cioé tale che
con P definita positiva che sia strettamente decrescente nel tempo
(cioé tale che 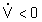 [DV]<0)
qualora il sistema evolva per moto libero da uno stato iniziale
[DV]<0)
qualora il sistema evolva per moto libero da uno stato iniziale 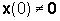 .
Inoltre, tale funzione esiste se e solo se l'equazione di Liapunov (25)
[(26)] ammette una soluzione (P,Q) con P e Q
definite positive. Infine, se una tale soluzione (P,Q) esiste
ne esistono infinite, una per ogni matrice Q definita positiva. .
Inoltre, tale funzione esiste se e solo se l'equazione di Liapunov (25)
[(26)] ammette una soluzione (P,Q) con P e Q
definite positive. Infine, se una tale soluzione (P,Q) esiste
ne esistono infinite, una per ogni matrice Q definita positiva. |
L'ultima affermazione del teorema di Liapunov
permette di ricavare un criterio operativo per la verifica dell'asintotica
stabilità di un sistema di cui sia assegnata la matrice A.
Fissata a caso una matrice Q simmetrica e definita positiva nell'equazione
di Liapunov (per esempio Q=I (matrice identità)),
si risolve l'equazione nell'incognita P (si noti che si tratta di
risolvere un sistema di n(n+1)/2 equazioni lineari in altrettante incognite,
dato che P deve essere simmetrica): se la soluzione esiste e P
è definita positiva (cosa che si può appurare con il criterio
di Sylvester) il sistema è asintoticamente stabile.
Si noti che il teorema di Liapunov non
afferma né richiede alcunché sulla struttura della matrice
P.
Non raro è, tuttavia, il caso in cui P è diagonale,
cioè il caso in cui la funzione di Liapunov V(x) non contiene
termini misti xixj con 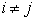 (di questo tipo è, ad esempio, la funzione energia delle reti elettriche).
Quando ciò accade, cioé quando l'equazione di Liapunov ammette
una soluzione (P,Q) con P e Q definite positive
e con P diagonale, il sistema, oltre a essere asintoticamente stabile,
rimane tale per qualsiasi perturbazione strutturale (teorema di Arrow-McManus).
Ciò significa che se esiste una matrice P diagonale con pij>0,
i=1,...,n tale che la matrice
(di questo tipo è, ad esempio, la funzione energia delle reti elettriche).
Quando ciò accade, cioé quando l'equazione di Liapunov ammette
una soluzione (P,Q) con P e Q definite positive
e con P diagonale, il sistema, oltre a essere asintoticamente stabile,
rimane tale per qualsiasi perturbazione strutturale (teorema di Arrow-McManus).
Ciò significa che se esiste una matrice P diagonale con pij>0,
i=1,...,n tale che la matrice 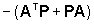 sia definita positiva, non solo è asintoticamente stabile il sistema
sia definita positiva, non solo è asintoticamente stabile il sistema 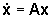 ma anche qualsiasi sistema del tipo
ma anche qualsiasi sistema del tipo 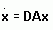 con D diagonale e
con D diagonale e 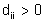 .
In altre parole, il sistema .
In altre parole, il sistema 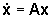 è asintoticamnete stabile e rimane tale sotto l'effetto di qualsiasi
perturbazione che abbia come conseguenza la moltiplicazione di ogni sua
equazione di stato per una costante positiva e arbitraria.
è asintoticamnete stabile e rimane tale sotto l'effetto di qualsiasi
perturbazione che abbia come conseguenza la moltiplicazione di ogni sua
equazione di stato per una costante positiva e arbitraria. |