Possiamo ora
riprendere e approfondire il tema, già trattato nel Paragrafo
B.3, della determinazione del modello
ARMA di un assegnato sistema 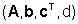 .
Ricordiamo per questo che un modello ARMA è individuato da una
coppia di polinomi (N(p), D(p)) che identificano univocamente l'equazione
(7), la quale, a seconda che il tempo sia discreto o continuo, è
l'equazione alle differenze (5) o l'equazione differenziale (6). Ricordiamo
anche che il modello ARMA si dice ridotto [non ridotto] se i polinomi
N(p) e D(p) sono [non sono] primi tra loro. Inoltre, il rapporto tra i
due polinomi N(p) e D(p) è chiamato funzione
di trasferimento e indicato con G(p), cioè .
Ricordiamo per questo che un modello ARMA è individuato da una
coppia di polinomi (N(p), D(p)) che identificano univocamente l'equazione
(7), la quale, a seconda che il tempo sia discreto o continuo, è
l'equazione alle differenze (5) o l'equazione differenziale (6). Ricordiamo
anche che il modello ARMA si dice ridotto [non ridotto] se i polinomi
N(p) e D(p) sono [non sono] primi tra loro. Inoltre, il rapporto tra i
due polinomi N(p) e D(p) è chiamato funzione
di trasferimento e indicato con G(p), cioè
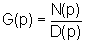
Ovviamente, conoscere la funzione di trasferimento
G(p) non significa conoscere il modello ARMA (N(p), D(p)), a meno che questo
sia ridotto.
Poiché il modello ARMA rappresenta
le relazioni intercorrenti tra ingresso e uscita nel caso generale di stato
iniziale qualsiasi, esso deve per forza essere associato alle sole parti
osservabili (parti (b) e (d)) del sistema, che per chiarezza riportiamo
in Fig. 16 estraendole dalla Fig. 15 del paragrafo precedente.
 |
|
Figura 16 Parti
osservabili (b) e (d) di un sistema
|
Per quanto visto nel secondo e terzo paragrafo,
il primo dei due sottosistemi (quello che determina la componente yb
dell'uscita) è descritto dal modello ARMA a molti ingressi
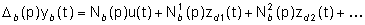 (28)
(28)
Dove Db(p)
è il polinomio caratteristico di Ab e 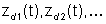 sono le componenti del vettore di stato zd(t), che fungono
da ingressi. Il secondo sottosistema (quello che determina la componente
yd dell'uscita) è, invece, senza ingressi ed è,
quindi, descritto dal modello AR
sono le componenti del vettore di stato zd(t), che fungono
da ingressi. Il secondo sottosistema (quello che determina la componente
yd dell'uscita) è, invece, senza ingressi ed è,
quindi, descritto dal modello AR
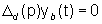 (29)
(29)
dove Db(p)
è il polinomio caratteristico di Ad. Inoltre,
datto che ogni componente del vettore di stato zd(t) può
essere interpretata come una uscita del secondo sottosistema, deve essere
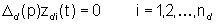 (30)
(30)
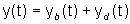 ,
si ottiene ,
si ottiene
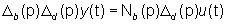
Il modello ARMA del sistema è, quindi,
non ridotto perché
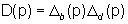
e
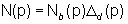
non sono primi tra loro.
Se, invece, la parte (d) è mancante, cioè
se il sistema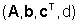 non
ha parte non raggiungibile e osservabile, allora il modello ARMA non
ha parte non raggiungibile e osservabile, allora il modello ARMA
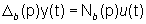
è in forma ridotta perché si può
verificare che Db(p)
e Nb(p) sono primi tra loro (essendo la parte (b) completamente raggiungibile
e osservabile). Si può così concludere con il seguente teorema.

In molti casi di interesse pratico il modello 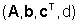 del sistema non è noto, ma si conoscono una coppia u(.)
e y(.) di funzioni d'ingresso e uscita rilevata
sperimentalmente per un certo periodo di tempo [0,t). È questo,
ad esempio, il caso di un bacino idrico del quale siano stati rilevati
la precipitazione e il deflusso nel punto di chiusura del bacino per un
periodo di qualche mese, o il caso di un amplificatore elettrico di cui
siano stati registrati i segnali di ingresso e uscita per qualche secondo.
È lecito chiedersi se è possibile, in questi casi, determinare
un modello
del sistema non è noto, ma si conoscono una coppia u(.)
e y(.) di funzioni d'ingresso e uscita rilevata
sperimentalmente per un certo periodo di tempo [0,t). È questo,
ad esempio, il caso di un bacino idrico del quale siano stati rilevati
la precipitazione e il deflusso nel punto di chiusura del bacino per un
periodo di qualche mese, o il caso di un amplificatore elettrico di cui
siano stati registrati i segnali di ingresso e uscita per qualche secondo.
È lecito chiedersi se è possibile, in questi casi, determinare
un modello 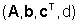 del sistema elaborando le registrazioni di ingresso e uscita. Questo problema
è, in generale, noto come problema dell'identificazione
del modello ed è di importanza basilare nelle applicazioni. Per
motivi di realismo, esso viene spesso affrontato supponendo che le misure
di ingresso e/o di uscita siano affette da rumore a carattere più
o meno aleatorio, così che la soluzione del problema richiede nozioni,
a volte anche non elementari, di statistica e di teoria dei processi stocastici.
Il problema risulta tuttavia concettualmente e operativamente interessante
anche nella sua versione più semplice che è quella in cui,
oltre all'assenza di rumore, si ipotizzi che il sistema sia lineare, proprio,
a tempo discreto e con dimensione no=nb+nd
delle parti osservabili nota. In tale ipotesi, il modello ARMA del
sistema è
del sistema elaborando le registrazioni di ingresso e uscita. Questo problema
è, in generale, noto come problema dell'identificazione
del modello ed è di importanza basilare nelle applicazioni. Per
motivi di realismo, esso viene spesso affrontato supponendo che le misure
di ingresso e/o di uscita siano affette da rumore a carattere più
o meno aleatorio, così che la soluzione del problema richiede nozioni,
a volte anche non elementari, di statistica e di teoria dei processi stocastici.
Il problema risulta tuttavia concettualmente e operativamente interessante
anche nella sua versione più semplice che è quella in cui,
oltre all'assenza di rumore, si ipotizzi che il sistema sia lineare, proprio,
a tempo discreto e con dimensione no=nb+nd
delle parti osservabili nota. In tale ipotesi, il modello ARMA del
sistema è
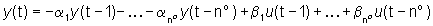
e può essere scritto nella forma
più compatta
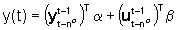 (31)
dopo aver definito i vettori
(31)
dopo aver definito i vettori
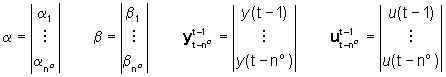
Se supponiamo, allora, che sia nota una serie temporale
di N valori successivi di ingresso e uscita
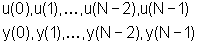
possiamo scrivere la relazione (31) nelle 2n0
incognite aie
bi,
i=1,
n0, per N-n0 valori successivi di t, precisamente
per 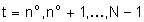 .
Ciò porta al seguente sistema di N-n0 equazioni in
2n0 incognite .
Ciò porta al seguente sistema di N-n0 equazioni in
2n0 incognite
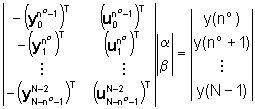
Questo è un sistema lineare del
tipo
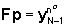 (32)
dove p è il vettore incognito
dei parametri ai
e biche
individuano il modello ARMA e F è una matrice dipendente
dai dati d'ingresso e uscita di dimensioni
(32)
dove p è il vettore incognito
dei parametri ai
e biche
individuano il modello ARMA e F è una matrice dipendente
dai dati d'ingresso e uscita di dimensioni 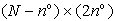 .
Perché tale sistema sia risolubile rispetto a p, casi critici
a parte, è quindi necessario che sia .
Perché tale sistema sia risolubile rispetto a p, casi critici
a parte, è quindi necessario che sia
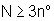
Nel caso in cui N=3n0 la soluzione
è
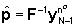
mentre nel caso N>3n0 la soluzione
può essere scritta nella forma
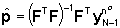 (33)
(33)
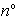 colonne
della matrice F sono tra loro identiche perché l'uscita
[l'ingresso] non varia nel tempo. Un altro caso di non identificabilità
si verifica quando lo stato iniziale zd(0) della parte non
raggiungibile e osservabile è nullo. In tale caso, infatti, il
segnale di uscita non risente assolutamente della parte (d) del sistema
(si veda la Fig. 16), così che i coefficienti del polinomio
caratteristico colonne
della matrice F sono tra loro identiche perché l'uscita
[l'ingresso] non varia nel tempo. Un altro caso di non identificabilità
si verifica quando lo stato iniziale zd(0) della parte non
raggiungibile e osservabile è nullo. In tale caso, infatti, il
segnale di uscita non risente assolutamente della parte (d) del sistema
(si veda la Fig. 16), così che i coefficienti del polinomio
caratteristico 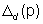 non sono identificabili. Ciò significa che non è identificabile
il modello ARMA del sistema dato che
non sono identificabili. Ciò significa che non è identificabile
il modello ARMA del sistema dato che 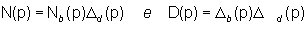 .
Quanto detto si può riassumere con il seguente teorema. .
Quanto detto si può riassumere con il seguente teorema.

Il modello ARMA di un sistema lineare
proprio e a tempo discreto di cui sia nota la dimensione n0=nb+nd
delle parti osservabili non può essere identificato da una serie
di N dati di ingresso e uscita se N<3n0. Se,
invece, 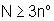 il modello ARMA risulta essere univocamente identificato, eccezion fatta
per alcuni casi critici (detti di non identificabilità).
il modello ARMA risulta essere univocamente identificato, eccezion fatta
per alcuni casi critici (detti di non identificabilità). |
A completamento e qualifica di quanto detto, facciamo due osservazioni,
una di interesse concettuale e l'altra di interesse operativo. Innanzitutto
notiamo che, una volta che il modello ARMA sia stato identificato, è
possibile costruire una terna 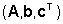 ,
che lo realizzi. Tale terna è quella in forma canonica di ricostruzione ,
che lo realizzi. Tale terna è quella in forma canonica di ricostruzione
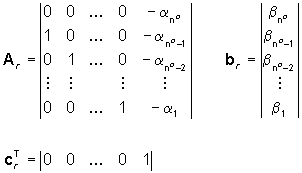
Infatti, per il Teorema 17, tale sistema è
completamente osservabile per cui non può che essere costituito
dalle parti (b) e (d) che qualificano, appunto, il modello ARMA. Se il
modello ARMA è in forma ridotta, cioè se i polinomi
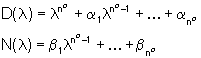
sono primi tra loro, la terna 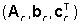 è anche completamente raggiungibile, cioè è costituita
dalla sola parte (b). Se, invece, il modello ARMA non è in forma
ridotta, cioè è del tipo
è anche completamente raggiungibile, cioè è costituita
dalla sola parte (b). Se, invece, il modello ARMA non è in forma
ridotta, cioè è del tipo
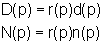
allora il sistema 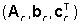 è costituito da una parte raggiungibile e osservabile con modello
ARMA dato da (n(p),d(p)) e da una parte non raggiungibile e osservabile
descritta da un modello MA individuato dal polinomio r(p) (che coincide
col polinomio caratteristico
è costituito da una parte raggiungibile e osservabile con modello
ARMA dato da (n(p),d(p)) e da una parte non raggiungibile e osservabile
descritta da un modello MA individuato dal polinomio r(p) (che coincide
col polinomio caratteristico 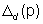 di tale parte).
di tale parte).
La terna in forma canonica di controllo
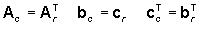
ottenuta per dualità dalla realizzazione
in forma canonica di ricostruzione, non è invece una realizzazione
del modello ARMA (N(p),D(p)), se tale modello non è in forma
ridotta. Il sistema 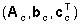 è, infatti, completamente raggiungibile (si veda il Teorema 13) per cui non può essere costituito dalle due parti (b)
e (d). La conclusione è, pertanto, che la forma canonica di controllo
è, infatti, completamente raggiungibile (si veda il Teorema 13) per cui non può essere costituito dalle due parti (b)
e (d). La conclusione è, pertanto, che la forma canonica di controllo 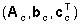 ha un modello ARMA individuato da (n(p),d(p)) anzichè da (N(p),D(p)):
essa realizza, quindi, soltanto la funzione di trasferimento G(p)=(N(p)/D(p))
ma non il modello ARMA nella sua interezza. Naturalmente, nel caso il
sistema sia completamente raggiungibile e osservabile, il modello ARMA
è in forma ridotta e la terna in forma canonica di controllo
è una sua realizzazione.
ha un modello ARMA individuato da (n(p),d(p)) anzichè da (N(p),D(p)):
essa realizza, quindi, soltanto la funzione di trasferimento G(p)=(N(p)/D(p))
ma non il modello ARMA nella sua interezza. Naturalmente, nel caso il
sistema sia completamente raggiungibile e osservabile, il modello ARMA
è in forma ridotta e la terna in forma canonica di controllo
è una sua realizzazione.
La seconda osservazione consiste nel notare
che, qualora ingressi e uscite siano stati rilevati commettendo degli errori,
la (32) dovrà per forza di cose essere sostituita dalla relazione
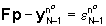
dove il vettore e rappresenta gli
scostamenti tra le previsioni dell'uscita effettuabili con il modello
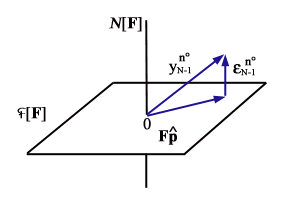
ARMA e i valori misurati delle uscite. La Fig. 18 mostra, nello
spazio di dimensioni N-n0, il vettore delle uscite misurate
e il sottospazio 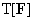 delle uscite prevedibili con un modello ARMA. È allora spontaneo
scegliere quel modello ARMA, cioè quel valore
delle uscite prevedibili con un modello ARMA. È allora spontaneo
scegliere quel modello ARMA, cioè quel valore 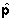 di p, che minimizza in questo spazio la distanza tra il vettore
delle uscite misurate e il vettore
di p, che minimizza in questo spazio la distanza tra il vettore
delle uscite misurate e il vettore 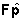 . .
|
| Figura 18 Illustrazione del
principio di stima ai minimi quadrati |
Come illustrato in figura ciò equivale
a scegliere 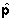 in modo tale che il vettore
in modo tale che il vettore 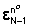 sia ortogonale a T[F]. Ma poichè
sia ortogonale a T[F]. Ma poichè 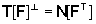 ciò equivale a imporre che
ciò equivale a imporre che
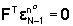
cioè
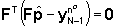
da cui segue (ipotizzando che 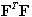 sia invertibile)
sia invertibile)
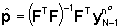
che è la formula (33).
La stima 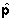 data dalla (33) è nota come stima ai minimi quadrati perché
è quella che, minimizzando la norma del vettore errore, minimizza
la somma dei quadrati degli scostamenti esistenti tra previsioni e misure.
Questa stima qui interpretata esclusivamente in termini geometrici,
gode di numerose proprietà per particolari caratteristiche statistiche
degli errori di misura di ingresso e/o uscita. Inoltre, la formula (33)
può essere utilmente resa ricorsiva, in modo che il calcolo della
stima di
data dalla (33) è nota come stima ai minimi quadrati perché
è quella che, minimizzando la norma del vettore errore, minimizza
la somma dei quadrati degli scostamenti esistenti tra previsioni e misure.
Questa stima qui interpretata esclusivamente in termini geometrici,
gode di numerose proprietà per particolari caratteristiche statistiche
degli errori di misura di ingresso e/o uscita. Inoltre, la formula (33)
può essere utilmente resa ricorsiva, in modo che il calcolo della
stima di 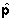 possa essere aggiornato in tempo reale, man mano che viene effettuata
una nuova misura, senza dover ogni volta invertire una matrice di dimensioni
possa essere aggiornato in tempo reale, man mano che viene effettuata
una nuova misura, senza dover ogni volta invertire una matrice di dimensioni 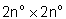 . .
|