Prima di introdurre le nozioni di serie di Fourier
e di trasformata di Fourier si ricordano alcune definizioni e risultati
cui si farà riferimento in seguito.

Le funzioni a variazione limitata godono di
un certo numero di proprietà che vengono ora riportate senza dimostrazione.

Ricordate queste proprietà, si può
ora riportare il primo importante risultata, quello della serie di Fourier.
Da un punto di vista intuitivo, tale risultato afferma che sotto ipotesi
molto generali una funzione periodica di periodo T può essere rappresentata
come combinazione lineare di sinusoidi di pulsazione pari a multipli della
pulsazione 2p/T.
Benchè questo risultato sia fondamentale in analisi matematica,
esso non facilmente dimostrabile per cui viene qui riportato senza dimostrazione.

Ovviamente, se la funzione 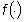 è continua nel punto t la (38) si semplifica e diventa
è continua nel punto t la (38) si semplifica e diventa
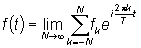 |
(40) |
Ricordando poi che :
dalle (39) e (40) si può facilmente ottenere
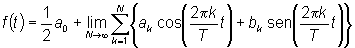 |
(41) |
dove
La (41) è l弾spressione forse più nota
della serie di Fourier perché mostra esplicitamente come la funzione 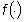 possa essere intesa come la combinazione lineare di sinusoidi e cosinusoidi.
Si può inoltre dimostrare che se
possa essere intesa come la combinazione lineare di sinusoidi e cosinusoidi.
Si può inoltre dimostrare che se 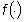 è una funzione tale che
è una funzione tale che
vale la seguente relazione:
dove i coefficienti fk sono dati dalla
(39).
Se si interpreta una funzione qualsiasi 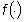 come una funzione periodica di periodo infinito, si può capire dai
risultati precedenti che per rappresentare tale funzione
come una funzione periodica di periodo infinito, si può capire dai
risultati precedenti che per rappresentare tale funzione 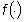 come combinazione lineare di sinusoidi e cosinusoidi sia necessario far
ricorso ad un continuo di frequenze poiché la pulsazione 2p/T
tende a zero qualora T tenda all段nfinito. È questa l段dea
di base della cosiddetta trasformazione di Fourier che verrà ora
precisata.
come combinazione lineare di sinusoidi e cosinusoidi sia necessario far
ricorso ad un continuo di frequenze poiché la pulsazione 2p/T
tende a zero qualora T tenda all段nfinito. È questa l段dea
di base della cosiddetta trasformazione di Fourier che verrà ora
precisata.
Sia 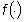 una funzione a variazione limitata su R e si supponga che tale funzione
soddisfi la relazione
una funzione a variazione limitata su R e si supponga che tale funzione
soddisfi la relazione
Si indichi, poi, con 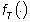 la funzione periodica di periodo T che coincide con
la funzione periodica di periodo T che coincide con 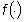 nell段ntervallo [-T/2,T/2). Per quanto detto in precedenza,
nell段ntervallo [-T/2,T/2). Per quanto detto in precedenza, 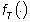 ammette uno sviluppo in serie di Fourier del tipo
ammette uno sviluppo in serie di Fourier del tipo
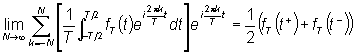 |
(42) |
Poichè, per definizione, 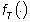 e
e 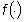 coincidono
nell'intervallo [-T/2,T/2) la relazione (42) può anche
essere scritta con f(t) al posto di fT(t) pur
di limitare t ad appartenere all'intervallo [-T/2,T/2).
Posto, allora, coincidono
nell'intervallo [-T/2,T/2) la relazione (42) può anche
essere scritta con f(t) al posto di fT(t) pur
di limitare t ad appartenere all'intervallo [-T/2,T/2).
Posto, allora,
dalla (39) per 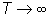 si
ottiene si
ottiene
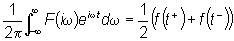 |
(43) |
e
La funzione 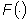 ora definita si chiama trasformata di Fourier o integrale di Fourier
della funzione
ora definita si chiama trasformata di Fourier o integrale di Fourier
della funzione 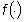 . .
|

