Si supponga che una funzione 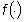 sia a variazione
limitata in ogni intervallo chiuso contenuto in
sia a variazione
limitata in ogni intervallo chiuso contenuto in 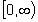 e che esista una costante
e che esista una costante 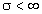 tale che
tale che
Si consideri, allora, la seguente funzione 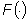
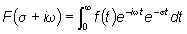 |
(44) |
e si noti che
cioè che tale funzione 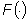 è la trasformata di Fourier della funzione
è la trasformata di Fourier della funzione
Pertanto, dalla (43) segue che
e
per t > 0. Indicando con s la variabile
complessa (cioè s = s
+ iw) la (44)
diventa
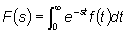 |
(45) |
e la funzione 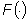 ,
spesso indicata con ,
spesso indicata con 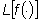 si chiama trasformata di Laplace della funzione
si chiama trasformata di Laplace della funzione 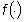 . .
Tale funzione 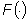 è una funzione complessa definita nel dominio Re(s)
> s0 dove
s0
è
il più piccolo numero reale tale che s
< s0
implichi
è una funzione complessa definita nel dominio Re(s)
> s0 dove
s0
è
il più piccolo numero reale tale che s
< s0
implichi
La trasformazione di Laplace 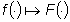 definita dalla (45) gode di un certo umero di proprietà. Innanzitutto,
tale trasformazione è lineare poichè
definita dalla (45) gode di un certo umero di proprietà. Innanzitutto,
tale trasformazione è lineare poichè
Inoltre, la trasformata di Laplace 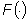 di una qualsiasi funzione
di una qualsiasi funzione 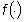 è una funzione analitica nel suo dominio di definizione Re(s)>s0.
Questo significa che la funzione
è una funzione analitica nel suo dominio di definizione Re(s)>s0.
Questo significa che la funzione 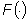 può spesso essere estesa all’intero piano complesso, nel senso che
esiste ed è unica una funzione coincidente con
può spesso essere estesa all’intero piano complesso, nel senso che
esiste ed è unica una funzione coincidente con 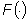 per Re(s)>s0
ma definita sull’intero piano complesso e ovunque analitica, ad eccezione
di un certo numero di punti isolati di singolarità. Ad esempio,
se f(t) = et,
per Re(s)>s0
ma definita sull’intero piano complesso e ovunque analitica, ad eccezione
di un certo numero di punti isolati di singolarità. Ad esempio,
se f(t) = et, 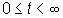 si ha
si ha
e la funzione 1 / (s-1) è
ovunque analitica con l'eccezione del punto singolare s = 1.
Altre importanti proprietà della
trasformata di Laplace sono quelle che mostrano come le operazioni di integrazione
e di derivazione di una funzione 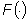 si trasformino in operazioni algebriche sulla trasformata
si trasformino in operazioni algebriche sulla trasformata 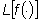 .
Valgono, infatti, le due seguenti relazioni .
Valgono, infatti, le due seguenti relazioni
Infine, l’operazione di prodotto di due
trasformate corrisponde, nel dominio del tempo, all’operazione detta di
convoluzione,e
cioè se 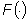 e
e 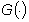 sono le trasformate
di Laplace di due funzioni sono le trasformate
di Laplace di due funzioni 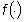 e
e 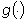 l’antitrasformata
della funzione l’antitrasformata
della funzione
è data da
A titolo di esempio, vengono qui di seguito
riportate alcune trasformate di Laplace F(s) di funzioni f(t).
|

