Per una larga classe di sistemi lineari a tempo
continuo il movimento periodico di uscita corrispondente ad un ingresso
sinusoidale è unico ed è anch'esso di tipo sinusoidale e
della stessa frequenza. Questa proprietà porta direttamente alla
definizione di risposta in frequenza e alla possibilità di
determinare la funzione
di trasferimento per mezzo di semplici prove da effettuare sul sistema.
Per quanto riguarda il problema dell'esistenza e
dell'unicità di un regime periodico, vale il seguente risultato:

I sistemi lineari a tempo continuo (A,b,cT)
che non hanno autovalori con parte reale nulla godono della proprietà
che ad ogni funzione d'ingresso 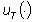 periodica e di periodo T è associata una ed una sola funzione
di uscita
periodica e di periodo T è associata una ed una sola funzione
di uscita 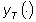 periodica
e dello stesso periodo. periodica
e dello stesso periodo.
Inoltre, se la parte osservabile è asintoticamente
stabile l'uscita y(t) del sistema conseguente all'applicazione dell'ingresso 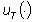 tende asintoticamente verso
tende asintoticamente verso 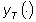 qualsiasi sia lo stato iniziale x(0) del sistema.
qualsiasi sia lo stato iniziale x(0) del sistema. |
Per verificare che questo teorema non possa
essere esteso al caso dei sistemi con autovalori con parte reale nulla
(sistemi non iperbolici) è sufficiente considerare il caso di un
integratore 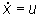 ,
y=
x. Infatti, in un tale sistema all’ingresso cosinusoidale ,
y=
x. Infatti, in un tale sistema all’ingresso cosinusoidale
corrispondono infinite uscite periodiche 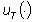 , ,
dove a
è una costante arbitraria (pari allo stato iniziale x(0)
del sistema).
Tra tutte le funzioni periodiche 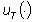 sono di particolare interesse le funzioni sinusoidali
sono di particolare interesse le funzioni sinusoidali
perchè è noto che sotto ipotesi
molto generali (vedi prossimo paragrafo) ogni funzione periodica 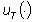 di periodo T può essere sviluppata in serie di Fourier ed espressa
come combinazione lineare di sinusoidi e cosinusoidi di pulsazione n(2p/t),
n intero non negativo. Se
di periodo T può essere sviluppata in serie di Fourier ed espressa
come combinazione lineare di sinusoidi e cosinusoidi di pulsazione n(2p/t),
n intero non negativo. Se 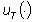 è una funzione periodica di periodo T si ha, infatti
è una funzione periodica di periodo T si ha, infatti
dove:
Pertanto la funzione periodica 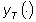 corrispondente ad un ingresso periodico
corrispondente ad un ingresso periodico 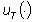 può essere calcolata determinando dapprima le componenti dello sviluppo
in serie di Fourier di
può essere calcolata determinando dapprima le componenti dello sviluppo
in serie di Fourier di 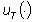 e poi sommando tutte le corrispondenti funzioni periodiche di uscita (principio
di sovrapposizione degli effetti). Inoltre, l'interesse per le funzioni
sinusoidali è motivato dai risultati che seguono.
e poi sommando tutte le corrispondenti funzioni periodiche di uscita (principio
di sovrapposizione degli effetti). Inoltre, l'interesse per le funzioni
sinusoidali è motivato dai risultati che seguono.

I sistemi lineari a tempo continuo (A,b,cT)
che non hanno autovalori con parte e nulla godono della proprietà
che ad ogni funzione d’ingresso del tipo
è assoociata una ed una sola funzione
di uscita 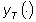 periodica, anch'essa sinusoidale e della stessa pulsazione 2p/T,
cioè
periodica, anch'essa sinusoidale e della stessa pulsazione 2p/T,
cioè
Inoltre, Y è lineare in U e
j dipende soltanto da w,
cioè
|
Questo teorema afferma che la risposta
ad una sinusoide di pulsazione w
e ampiezza unitaria è una sinusoide di ampiezza R(w)
sfasata di j(w)
rispetto alla precedente.
Pertanto, il calcolo della funzione periodica 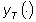 corrispondente ad un ingresso periodico
corrispondente ad un ingresso periodico 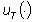 è di immediata esecuzione una volta che si conoscano le due funzioni
è di immediata esecuzione una volta che si conoscano le due funzioni 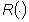 e
e 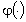 . A questa
coppia di funzioni si dà, per ovvi motivi, il nome di risposta
in frequenza. . A questa
coppia di funzioni si dà, per ovvi motivi, il nome di risposta
in frequenza.
La risposta in frequenza di un sistema
può spesso essere facilmente rilevata per mezzo di semplici prove
effettuate sul sistema. Infatti, si supponga di aver a che fare con un
sistema asintoticamente stabile (a rigore, come detto nel Teorema
25, è sufficiente l’asintotica stabilità della parte osservabile)
e si applichi in ingresso una sinusoide di ampiezza U e pulsazione w.
Pur di lasciar trascorrere un periodo di tempo sufficientemente elevato,
è allora possibile determinare la coppia (R(w),
j(w))
semplicemente misurando le ampiezze U e Y delle sinusoidi di ingresso e
di uscita e lo sfasamento j(w)
tra queste due sinusoidi.
Qualora il sistema non abbia la parte osservabile
asintoticamente stabile non è, in generale, più possibile
rilevare sperimentalmente la risposta in frequenza del sistema perché
l’uscita tende asintoticamente alla sinusoide 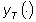 solo per un valore molto particolare dello stato iniziale. Pur tuttavia,
questo non significa, come affermato da alcuni, che la risposta in frequenza
non sia definibile in questo caso: il problema della definibilità
di una grandezza è infatti ben distinto dal problema della sua determinabilità.
La risposta in frequenza di un sistema può essere graficamente rappresentata
in due modi: o per mezzo dei due diagrammi cartesiani delle funzioni
solo per un valore molto particolare dello stato iniziale. Pur tuttavia,
questo non significa, come affermato da alcuni, che la risposta in frequenza
non sia definibile in questo caso: il problema della definibilità
di una grandezza è infatti ben distinto dal problema della sua determinabilità.
La risposta in frequenza di un sistema può essere graficamente rappresentata
in due modi: o per mezzo dei due diagrammi cartesiani delle funzioni 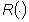 e
e 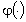 o per
mezzo di un diagramma polare rappresentante la funzione o per
mezzo di un diagramma polare rappresentante la funzione 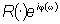 ( in quest’ultimo caso si parla di diagrammi di Nyquist).
( in quest’ultimo caso si parla di diagrammi di Nyquist).
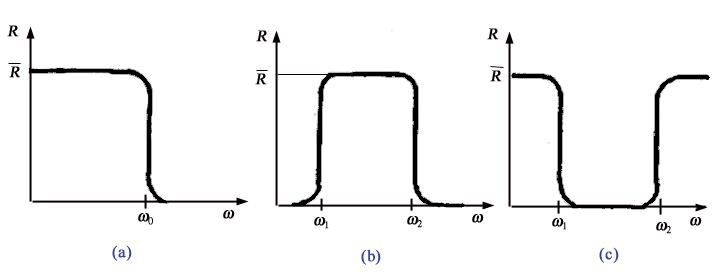
Tipici diagrammi cartesiani della funzione 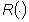 sono rappresentati in Fig. 25. In corrispondenza di alcune pulsazioni w
si ha
sono rappresentati in Fig. 25. In corrispondenza di alcune pulsazioni w
si ha 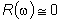 il che
corrisponde ad una forte attenuazione dell’ingresso. Così, ad esempio,
il sistema di Fig. 25a attenua tutte le sinusoidi di pulsazione maggiore
di w0
mentre le sinusoidi con w<w0
non
vengono attenuate. Questo tipo di sistema è pertanto detto passa
basso e l’intervallo [0,w0]
si chiama banda (ovviamente, non esistendo una discontinuità
in il che
corrisponde ad una forte attenuazione dell’ingresso. Così, ad esempio,
il sistema di Fig. 25a attenua tutte le sinusoidi di pulsazione maggiore
di w0
mentre le sinusoidi con w<w0
non
vengono attenuate. Questo tipo di sistema è pertanto detto passa
basso e l’intervallo [0,w0]
si chiama banda (ovviamente, non esistendo una discontinuità
in 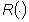 , cioè
non essendo R(w)
=1 per , cioè
non essendo R(w)
=1 per 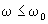 e R(w)
=0 per w>w0
la banda passante del sistema va definita in modo opportuno). Il sistema
con
e R(w)
=0 per w>w0
la banda passante del sistema va definita in modo opportuno). Il sistema
con 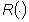 come in
Fig. 25b attenua, invece, le sinusoidi con pulsazione w<w1,
e quelle con pulsazione w>w2
ed è, pertanto detto passa banda. Per il motivo opposto il
sistema con come in
Fig. 25b attenua, invece, le sinusoidi con pulsazione w<w1,
e quelle con pulsazione w>w2
ed è, pertanto detto passa banda. Per il motivo opposto il
sistema con 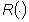 come in Fig. 25c è detto arresta banda.
come in Fig. 25c è detto arresta banda.
 |
|
Figura 25 Esempi
tipici di risposte in frequenza: (a) passa-basso; (b) passa-banda; (c)
arresta-banda.
|
Casi limite di notevole interesse si ottengono
facendo tendere a zero la banda di un sistema passa banda e di un sistema
arresta banda. Si ottengono così sistemi detti, rispettivamente,
filtri
risonatori e filtri a notch, che sono praticamente sensibili
o insensibili soltanto a una ben precisa pulsazione.
Naturalmente, non è soltanto di
interesse l'andamento della sola funzione 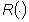 ma anche quello della funzione
ma anche quello della funzione 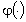 ,
anzi, solitamente è significativo l'andamento congiunto delle due
funzioni (cioè la risposta in frequenza). Ad esempio, si consideri
un sistema di comunicazione che, in condizioni ideali, dovrebbe essere
in grado di riprodurre in iscita una copia perfetta dell'ingresso, naturalmente
con un certo ritardo di tempo t
necessario per trasferire l'informazione dalla sezione di ingresso a quella
di uscita. Una sinusoide Usenwt
in
ingresso deve produrre, cioè, una sinusoide Usenw(t-t)
in
uscita, e questo deve essere verificato per tutte le pulsazioni w.
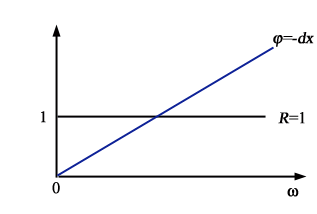
Ne
segue che tale sistema è caratterizzato da R(w)=1
j(w)=
-wt, come
mostrato in Fig.26. ,
anzi, solitamente è significativo l'andamento congiunto delle due
funzioni (cioè la risposta in frequenza). Ad esempio, si consideri
un sistema di comunicazione che, in condizioni ideali, dovrebbe essere
in grado di riprodurre in iscita una copia perfetta dell'ingresso, naturalmente
con un certo ritardo di tempo t
necessario per trasferire l'informazione dalla sezione di ingresso a quella
di uscita. Una sinusoide Usenwt
in
ingresso deve produrre, cioè, una sinusoide Usenw(t-t)
in
uscita, e questo deve essere verificato per tutte le pulsazioni w.
Ne
segue che tale sistema è caratterizzato da R(w)=1
j(w)=
-wt, come
mostrato in Fig.26.
|
|
Figura 26 Risposta
in frequenza di un sistema di comunicazione ideale
|
Tale sistema (ritardatore) non è realizzabile
per mezzo di un sistema lineare a dimensioni finite per cui spesso i sistemi
di comunicazione vengono progettati tollerando una certa distorsione tra
ingresso e uscita e, cioè, approssimando l’andamento delle funzioni 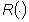 e
e 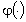 di Fig. 26
in un opportuno intervallo di pulsazioni. di Fig. 26
in un opportuno intervallo di pulsazioni.
Si è finora mostrato come la conoscenza della
risposta in frequenza (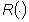 , ,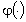 ) di un sistema lineare permetta di calcolare rapidamente la funzione periodica
di uscita corrispondente ad una funzione periodica di ingresso e come le
proprietà filtranti di un sistema possano facilmente essere dedotte
dall’analisi della sua risposta in frequenza. È poi stato mostrato
come la risposta in frequenza possa essere sperimentalmente rilevata (per
punti) per mezzo di prove da effettuare sul sistema qualora tale sistema
sia asintoticamente stabile. Queste proprietà sarebbero di per sè
già sufficienti a giustificare l’interesse dedicato all’argomento.
Tuttavia esiste un’ultima proprietà che, correlando la nozione di
risposta in frequenza con quella di funzione di trasferimento, rende ancor
più significativa la definizione di risposta in frequenza di un
sistema lineare.
) di un sistema lineare permetta di calcolare rapidamente la funzione periodica
di uscita corrispondente ad una funzione periodica di ingresso e come le
proprietà filtranti di un sistema possano facilmente essere dedotte
dall’analisi della sua risposta in frequenza. È poi stato mostrato
come la risposta in frequenza possa essere sperimentalmente rilevata (per
punti) per mezzo di prove da effettuare sul sistema qualora tale sistema
sia asintoticamente stabile. Queste proprietà sarebbero di per sè
già sufficienti a giustificare l’interesse dedicato all’argomento.
Tuttavia esiste un’ultima proprietà che, correlando la nozione di
risposta in frequenza con quella di funzione di trasferimento, rende ancor
più significativa la definizione di risposta in frequenza di un
sistema lineare.

La risposta in frequenza (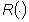 ,
,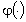 )
dI un sistema lineare a tempo continuo èunivocamente individuata
dalla funzione di trasferimento G(s) del sistema. Più precisamente
R(w)
e j(w)
sono, rispettivamente, il modulo e l’argomento dei numero complesso G(iw)
cioè )
dI un sistema lineare a tempo continuo èunivocamente individuata
dalla funzione di trasferimento G(s) del sistema. Più precisamente
R(w)
e j(w)
sono, rispettivamente, il modulo e l’argomento dei numero complesso G(iw)
cioè
|
La dimostrazione di questo teorema può essere
fatta verificando che le sinusoidi uT(t) = Usenwt
e yT(t) = R(w)Usen(wt+j(w))
con R(w) e
j(w)
legate a G(s) come indicato dalla (36) soddisfano l’equazione differenziale
(modello ARMA)
dove G(s) = n(s)/d(s). Ad esempio, se il sistema
è del primo ordine, cioè 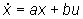 e y = x si ha:
e y = x si ha:
per cui il modello ARMA è
mentre la risposta in frequenza è:
E così immediato verificare (usando le formule
di prostaferesi) che le due sinusoidi
| uT(t) = Usenwt |
| yT(t) = R(w)Usen(wt+j(w)) |
soddisfano la (37).
ll risultato espresso dal Teorema 27 è estremamente
importante, poichè esso permette di calcolare la risposta in
frequenza di un sistema lineare assegnato per mezzo della terna (A,b,cT)
o del suo modello ARMA o della sua funzione di trasferimento G(s). Inoltre,
esso può essere la base per una soluzione relativamente semplice
del problema dell’identificazione (vedi).
Infatti, se si vuoi associare ad un ente fisico un modello si devono
effettuare alcune prove sul sistema e, in base all’esito di queste,
determinare ad esempio, la terna (A,b,cT).
Tali prove non possono essere altro che rilevazioni di coppie di funzioni
d’ingresso e uscita, quali, ad esempio la risposta all’impulso o la
risposta in frequenza. Da queste funzioni si deve poi risalire alla
funzione di trasferimento del sistema e, quindi, secondo quanto esposto
nel paragrafo
dedicato alla realizzazione, alla terna (A,b,cT).
Tra tutte le prove effettuabili sul sistema, la risposta in frequenza
è quella che presenta il minor numero di inconvenienti. Infatti
per effettuare il rilevamento della risposta in frequenza di un sistema
asintoticamente stabile non si deve inizialmente porre il sistema a
riposo (cioè x(0) può essere diverso dal vettore
nullo), mentre questo è necessario qualora si voglia rilevare
la risposta all’impulso o allo scalino del sistema. Inoltre, la risposta
in frequenza può essere rilevata applicando all’ingresso del
sistema sinusoidi di ampiezza relativamente limitata in modo che non
intervengano (o che per lo meno siano trascurabili) effetti non lineari
che immancabilmente sono presenti qualora. le funzioni d’ingresso assumano
valori elevati. Ovviamente, questo non è il caso qualora si effettui
il rilevamento della risposta all’impulso. Infine, qualora si applichi
al sistema una sinusoide e in uscita (a transitono esaurito) si ottenga
una forma d’onda periodica ma non sinusoidale si può concludere
che il sistema non può essere ragionevolmente descritto da equazioni
lineari; un tale risultato non si può facilmente ottenere esaminando
la risposta all’impulso poiche è estremamente complesso dire
se un oscillogramma è costituito da una combinazione lineare
di esponenziali oppure no.
|

