

L'ingresso di molti sistemi a tempo continuo
è a volte variato in istanti ben precisi e poi mantenuto costante
per intervalli di tempo più o meno lunghi e regolari. Ciò
può accadere in un sistema di produzione, il cui tasso di produzione
viene fissato con cadenza settimanale, nelle reazioni biochimiche indotte
da un farmaco somministrato per fleboclisi, il cui dosaggio viene stabilito
una volta al giorno, nello sfruttamento di una riserva idrica per produzione
di energia elettrica, in cui la portata da turbinare viene programmata
con cadenza oraria e in molti altri sistemi caratterizzati dalla presenza
di un decisore che, per motivi diversi, non ritiene opportuno intervenire
con continuità sul sistema. Presa la decisione in un certo istante,
l'ingresso del sistema (tasso di produzione, dosaggio del farmaco, portata
da turbinare) viene mantenuto costante per un certo intervallo di tempo,
alla fine del quale viene presa una nuova decisione. A differenza degli
ingressi, le variabili di stato caratterizzanti il sistema (scorte, concentrazioni,
riserve d'acqua) variano (e a volte consistentemente) durante questi intervalli
di tempo. Una situazione del tutto analoga si riscontra con sempre maggior
frequenza nell'automazione industriale, dove vengono usati calcolatori
per controllare vari processi: durante un certo intervallo di tempo il
calcolatore elabora le informazioni ricevute e determina il valore
Anche per quanto riguarda le variabili
di stato x e di uscita y, l'ipotesi che si fa per definire
i sistemi a segnali campionati è in linea con le moderne tecniche
di misura che "leggono" ripetutamente i valori Lo schema di campionamento più semplice,
indicato simbolicamente in Fig. 8, è caratterizzato dall'avere
gli stessi istanti di campionamento per tutte le variabili (stato e uscita)
e periodo
di campionamento T costante e coincidente con quello durante
il quale l'ingresso è mantenuto costante.
Campionamenti più complessi si hanno quando T non è costante nel tempo (campionamento casuale e campionamento adattativo), quando il periodo di campionamento non è lo stesso per tutte le variabili (campionamento a frequenza differenziata), quando, pur essendo T costante nel tempo e uguale per tutte le variabili, risultano tra loro sfasati gli istanti di campionamento (campionamento asincrono) o quando il circuito di mantenimento, anziché mantenere l'ingresso del sistema costante, lo fa variare secondo una legge prefissata (ad esempio, linearmente). Supponendo di essere nel caso più semplice, abbiamo quindi a che fare con un sistema a tempo continuo
con ingresso costante a tratti. Numerati
gli intervalli di campionamento con l'indice k=0,1,2,…, si possono allora
definire le variabili di ingresso
Applicando la formula
di Lagrange (20) al sistema a tempo continuo con istante iniziale kT
e istante finale (k+1)T, e tenendo conto che tra questi due istanti l'ingresso
è costante e pari a
Sostituendo in questa relazione x(kT)
e x((k+1)T) con
si ottiene allora che è l'equazione di stato del sistema a segnali campionati, interpretato come sistema a tempo discreto. Poiché, ovviamente, la trasformazione di uscita vale anche per le variabili campionate, si può concludere che un sistema a segnali campionati è un sistema a tempo discreto
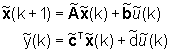 |
| Avanti |