n un sistema dinamico l'ingresso in un intervallo di tempo [0,t] e lo stato iniziale x(0) determinano univocamente lo stato x(t) e l'uscita y(t) all'istante finale t. In altre parole, l'evoluzione nel futuro del sistema è sempre garantita e univocamente individuata. Nel caso dei sistemi lineari ciò risulta evidente dalle formule di Lagrange (20) e (22) valide per 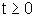. In alcuni sistemi l'evoluzione è garantita e univocamente individuata anche nel passato. Tali sistemi sono detti reversibili. Per i sistemi lineari vale il seguente risultato.

La dimostrazione di questo teorema segue dal fatto che nel caso dei sistemi a tempo continuo la matrice di transizione 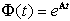 è invertibile (la sua inversa è, infatti, 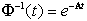). Nel caso dei sistemi a tempo discreto, invece, 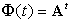 , per cui  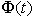è invertibile se e solo se 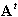 e, quindi, A è invertibile.
Il Teorema 3 lascia intravedere una forte analogia tra sistemi a tempo continuo e sistemi a tempo discreto reversibili. C'è invece da aspettarsi che i sistemi irreversibili a tempo discreto necessitino, in un certo senso, di maggior attenzione. La peculiarità della irreversibilità è spesso poco evidenziata anche perché i sistemi a tempo discreto che vengono discussi con maggior frequenza sono i sistemi a segnali campionati che, come vedremo nel prossimo paragrafo, sono reversibili. Esistono, tuttavia, importanti classi di sistemi a tempo discreto che sono irreversibili, come i sistemi a memoria finita che sono quelli in cui lo stato iniziale influenza l'evoluzione del sistema soltanto per un periodo di tempo finito. Poiché

in tali sistemi il movimento libero è nullo a partire da un certo istante, qualsiasi sia lo stato iniziale x(0). Ciò implica che det=F(t)=det(A^t)=det(A)^t=0, cioè l'irreversibilità.