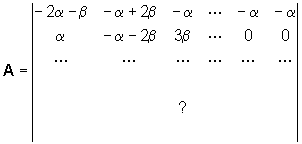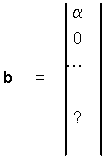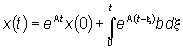|
L'occupazione delle
macchine è modellizzabile con un sistema lineare a tempo continuo e ingresso
unitario, in cui l'i-esima variabile di stato rappresenta la
probabilità che siano occupate i macchine.
Si può pertanto affermare che l'occupazione
delle macchine è a regime dopo un periodo pari a cinque volte la costante di
tempo dominante, mentre il numero medio di macchine occupate a regime risulta
essere uguale al guadagno del sistema.
IL MODELLO:
Si indichi con xi(t),
i=0,1,2,...,n, la probabilità che all'istante t della
giornata siano occupate i macchine (ovviamente  ,  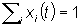), con adt la
probabilità di arrivo di un utente nell'intervallo di tempo (t, t+dt)
e con bdt la
probabilità che una macchina occupata all'istante t si liberi durante
l'intervallo di tempo di durata dt immediatamente successivo.
Trascurando gli eventi che hanno probabilità
proporzionale a (dt)3, si possono scrivere le seguenti
equazioni di bilancio:
|
Sostituendo x0
con
|
|
e facendo tendere dt
a zero, si ottiene allora:
|
|
Queste equazioni e
l'equazione
|
|
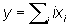
che definisce il numero
medio di macchine occupate, possono essere interpretate come
|
un sistema a tempo
continuo
con u=1 e:
TARATURA DEL MODELLO:
Perchè il modello sia completamente
individuato è necessario stimare (tarare) i due parametri a e b sulla
base delle informazioni disponibili.
Dimensionalmente, tali parametri sono delle
frequenze (tempo-1) e pertanto il loro valore dipende dall'unità
di tempo usata. Se, ad esempio, l'unità di tempo è l'ora, per ovvi motivi
risulta:
IL REGIME
STAZIONARIO:
All'apertura del centro di calcolo, tutte le
macchine sono libere e, quindi, x(0)=0.
Le probabilità xi(t)
varieranno quindi nel tempo e andranno asintoticamente ad assestarsi (dando
come scontato che il sistema sia asintoticamente
stabile) ad un valore di equilibrio  .
Durante il transitorio avremo quindi:
e il tempo T necessario per
raggiungere "in pratica" l'equilibrio  sarà pari a cinque
volte la massima costante di tempo Tmax del sistema.
Per determinare questa costante di tempo si
deve determinare l'autovalore dominante l*, dato che Tmax=-1/l*.
Se n>3, il calcolo di l* non è
banale, per cui è necessario ricorrere ad un package opportuno.
|
Per quanto riguarda il
calcolo del numero medio
|
|
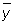
di macchine occupate a
regime, si può notare che
|
|
è l'uscita di equilibrio
|
|
corrispondente a
|
|
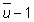
, per cui
|
|
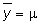
dove m è il
guadagno della funzione di trasferimento:
|
del sistema.
Di nuovo, il calcolo di m risulta
facilitato qualora si disponga di un package per il calcolo automatico delle funzioni di trasferimento.
|
