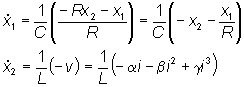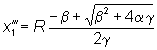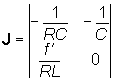EQUAZIONI DI STATO:

Le due equazioni di stato si scrivono immediatamente ricordando le leggi del condensatore e dell'induttore:
 

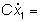	corrente nel condensatore
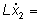	tensione sull'induttore

Nel caso specifico, tenendo conto che la tensione d'ingresso di un amplificatore operazionale è praticamente nulla, si ha:
 

Ma, d'altra parte, un amplificatore operazionale non assorbe corrente, per cui  i=x₂+(-x₂-x₁/R)=-x₁/R  e quindi:
 

EQUILIBRI E LORO STABILITA':
 

L'isoclina

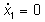è data da:

mentre l'isoclina

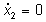è data da tre rette verticali nel piano di stato (vedi Fig.2)

X1"=0

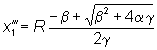La prima di queste tre rette sta sempre nel semipiano sinistro, mentre la terza sta sempre nel semipiano destro. 
Per tutti i valori dei parametri esistono pertanto tre equilibri: uno nel secondo quadrante, uno nell'origine ed uno nel quarto quadrante. 
 

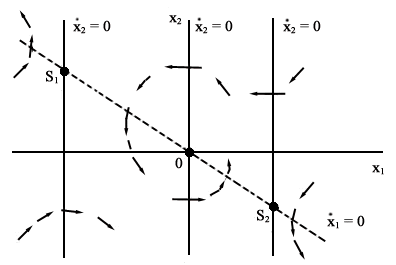Fig.2:  Isocline 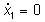  (---) e  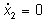(---), equilibri e verso delle traiettorie.  Gli equilibri S1 e S2 sono selle mentre l'origine è un fuoco o un nodo stabile.

Indicata con  v=f(i)  la caratteristica del BNL, e ricordando che  i=-x₁/R , lo Jacobiano del sistema può essere scritto nel modo seguente:
 

La traccia dello Jacobiano è quindi negativa in tutti e tre gli equilibri, mentre il determinante (f '/ RLC) risulta negativo nel primo e nel terzo stato di equilibrio e positivo nell'origine.
Si può, pertanto, concludere che l'origine è un fuoco o un nodo stabile (a seconda del valore dei parametri) e che gli altri due equilibri sono selle.

QUADRO DELLE TRAIETTORIE E BACINO DI ATTRAZIONE DELL'ORIGINE:
Poichè la funzione di Bendixon  non cambia segno in tutto lo spazio di stato (essendo pari a -1/RC) non esistono cicli limite.
Tenuto anche conto dell'inclinazione (facilmente determinabile) degli autovettori associati alle selle, si può inferire che il quadro delle traiettorie è come mostrato in Fig.3, dove sono riportate due possibili alternative.
 

Fig. 3: Collegamenti sella-fuoco, varietà stabili delle selle e bacino di attrazione dell'origine

Nel quadro di Fig.3a esistono due collegamenti sella-fuoco e il bacino di attrazione dell'origine è delimitato dalle varietà stabili delle due selle. 
Nel quadro di Fig.3b esiste invece un solo collegamento sella-fuoco e il bacino di attrazione dell'origine è delimitato dalla varietà stabile di una sola delle due selle. 
Se si ipotizza che entrambi i quadri siano possibili, significa che al variare di qualche parametro si deve passare dal primo al secondo quadro con continuità. Ciò implica che la varietà instabile della sella S₁ debba avvicinarsi sempre di più al variare del parametro alla sella S₂, fino ad andare in contatto con S₂ per un particolare valore del parametro. Per questo valore del parametro si ha un collegamento sella-sella (biforcazione) che, ovviamente, sparisce non appena il parametro viene ulteriormente variato, dando così luogo al secondo quadro.

Se si perturba la sola tensione x₁ sul condensatore, le perturbazioni che danno luogo a transitori che convergono verso l'equilibrio stabile sono quindi tutte quelle contenute nel segmento.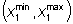 
Analogamente, se si perturba la sola corrente x₂, le perturbazioni ammissibili stanno sul segmento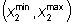di Fig.3. 
Tuttavia, se le perturbazioni di tensione dx₁e di corrente dx₂sono contemporanee, può accadere che la conseguente traiettoria perturbata tenda verso l'origine anche sedx₁edx₂sono molto grandi (perchè il bacino di attrazione non è limitato). Perturbazioni esterne al bacino di attrazione non sono "sopportabili" dalla rete poichè danno luogo a traiettorie che tendono all'infinito lungo le varietà instabili delle selle.

Nel caso interessi valutare il bacino di attrazione dell'origine, si potrebbe pensare di usare il criterio di La Salle che, come è noto, fornisce una stima per difetto del bacino di attrazione.
Nel caso in esame, l'applicazione del criterio di La Salle non è tuttavia semplice (dal punto di vista analitico). E' pertanto preferibile ricorrere all'uso di un opportuno package di simulazione, con il quale il problema può essere risolto in modo esatto senza grandi difficoltà. Infatti, poichè la frontiera del bacino di attrazione è costituita dalle varietà stabili delle selle, essa può essere determinata simulando il sistema all'indietro nel tempo (cioè integrando le equazioni di stato dopo averle cambiate di segno) a partire dai punti 1', 1", 2' e 2" nel caso di Fig.3a, e 2' e 2" nel caso di Fig.3b. 
Tali punti si possono facilmente trovare spostandosi di poco dai punti di sella S₁ e S₂ lungo gli autovettori stabili.