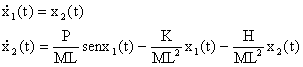|
Indicata
con x2(t) la velocità angolare dell’asta, con H il coefficiente
di attrito e ricordando che il momento d’inerzia del sistema è ML2
si ottiene:
Gli
stati di equilibrio si calcolano ponendo
in queste equazioni. Così
facendo, dalla prima si ha x2 = 0, per cui i valori x1
sono le soluzioni dell’equazione trascendente
Per
si ha un’unica soluzione (vedi figura), mentre per 
si hanno più soluzioni tra loro isolate.
Pertanto,
l’origine del1o spazio di stato è comunque uno stato di equilibrio
isolato di cui dobbiamo discutere la stabilità al variare del carico
P.
Per
studiare la stabilità dell’equilibrio x =0 SI determina dapprima
il sistema linearizzato
dove
Gli
autovalori del sistema linearizzato si ottengono risolvendo l'equazione
caratteristica
cioè
da
cui si ottiene
Pertanto,
per P<K/L, i due autovalori hanno parte reale negativa, mentre
per P > K/L un autovalore è positivo. Dal
teorema sulla linearizzazione segue che per P<K/L l’equilibrio considerato
è asintoticamente stabile, mentre per P>K/L esso è instabile.
In quest’ultimo caso se l’asta ferma e in posizione verticale viene perturbata
anche di pochissimo essa si allontana decisamente da tale posizione tendendo
ad un equilibrio completamente diverso. Per questo motivo il carico K/L
è detto “carico critico”.
|
