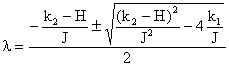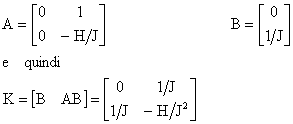|
Le
equazioni di stato dell’antenna sono
per
cui dato che
il
sistema nel complesso è descritto dalle equazioni
Gli
autovalori l1
e l2
del sistema risultante (2) sono le radici dell’equazione caratteristica
e
cioè
Tali
autovalori possono essere fissati ad arbitrio se è possibile determinare
i parametri k1 e k2 in modo tale che il polinomio
caratteristico (3) sia arbitrario, e ciò è evidentemente
possibile dato che i due parametri k1 e k2 influenzano
singolarmente i due coefficienti del polinomio caratteristico. Più
precisamente, se l1
e l2
sono i due autovalori desiderati, si deve porre
per
cui deve essere
L'esistenza
e l’unicità della coppia di parametri (k1, k2)
che permettono di fissare arbitrariamente gli autovalori del sistema regolato
è e priori garantita dalla completa
raggiungibilità del sistema (1) che ha
che
è in effetti una matrice non singolare.
E’
interessante confrontare il risultato qui ottenuto con quanto discusso
nel problema 21. In quel caso la coppia motrice u(t) dipendeva soltanto
dalla posizione angolare x1(t), cioè
 ,
mentre in questo caso si ha anche una dipendenza dalla velocità
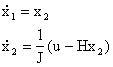
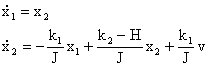x2(t). Consistentemente, in questo caso ai hanno migliori prestazioni:
infatti è possibile fissare ad arbitrio la dinamica del sistema
regolato, risultato che non era possibile conseguire con un controllore
esclusivamente sensibile all’errore angolare  .
|
(2)
(3)
