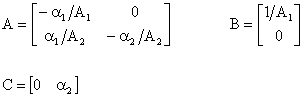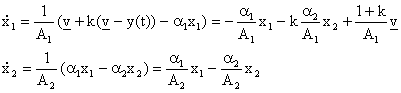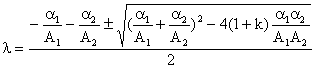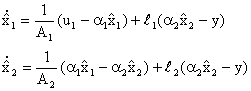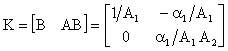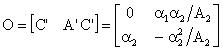|
Se
A1 eA2 sono le sezioni dei due serbatoi le equazioni
di stato sono
e
la trasformazione di uscita è
Il
sistema è quindi lineare
con matrici (A, B, C) date da
Gli
autovalori del sistema sono
e 
(la matrice A è triangolare per cui gli autovalori sono gli elementi
della diagonale) e all'equilibrio abbiamo  .Ad
una variazione istantanea dell’ingresso dal valore v1
al valore v2, corrisponde un transitorio di uscita di
tipo esponenziale (per la precisione una combinazione di esponenziali del
tipo 
ed  )
da 
che è appunto del tipo di quello indicato con (a) in figura.Per
avere transitori di tipo oscillatorio smorzato è necessario fare
in modo che il sistema abbia autovalori complessi e ciò può
essere effettivamente ottenuto comandando l'elettrovalvola per mezzo di
un semplice circuito che realizzi la seguente legge di controllo
dove
v
rappresenta la portata desiderata. Infatti, sostituendo la (2) nella (1)
si ottiene
che
è un sistema lineare con matrice A* data da
Gli
autovalori di A* sono le radici del polinomio caratteristico
per
cui
Ne
consegue che per
(cioè quando il “guadagno” dell’elettrovalvola è relativamente
basso) gli autovalori del sistema regolato sono ancora reali, mentreper
k>k* (cioè quando il “guadagno” dell'elettrovalvola è
elevato) gli autovalori sono complessi coniugati con parte reale negativa
(stabilità). Con la legge di controllo (2) è così
possibile ottenere transitori della portata di uscita del tipo di quello
indicato con (b) in figura. Tuttavia, periodo di oscillazione e smorzamento
non sono fissabili ad arbitrio. Infatti, solo uno dei coefficienti del
polinomio caratteristico (3) dipende da k cosi che i due autovalori 
hanno soltanto b che varia al variare di k. Ciò implica che dei
transitori di uscita (che sono del tipo  )
si può variare il periodo di oscillazione ( )
ma non lo smorzamento (a).Per
poter variare anche lo smorzamento dei transitori della portata di uscita
è necessario far uso di un circuito di comando dell’elettrovalvola
più complesso di quello corrispondente alla (2). Tale circuito può
essere un vero e proprio regolatore lineare costituito da una legge di
controllo lineare
e
da uno stimatore asintotico dello stato
Infatti,
il sistema (1) è completamente raggiungibile ed osservabi1e, dato
che le matrici
di raggiungibilità
e
di osservabilità
sono
non singolari, e ciò implica che tutti gli autovalori del sistema
(che sono in effetti quattro) possono essere arbitrariamente fissati. In
particolare, quindi, gli autovalori possono essere resi complessi coniugati
con parte reale ed immaginarla che soddisfino i requisiti voluti di smorzamento
e periodo dl oscillazione.
|
(1)
(2)
(3)
